Investigation of the Equation

by
Jennifer Roth

Using Algebra Expressor (Graphing Software) we can contruct different graphs for the equation

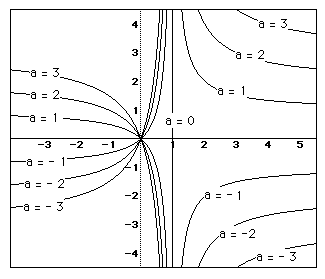
and we can overlay such graphs for different values of a, b, and c as the other two are held constant. From these graphs a pattern will develop.

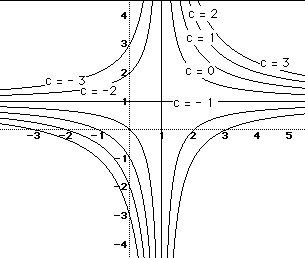
For example, if we set xy = x + y + c for c = -3, -2, -1, 0, 1, 2, 3, and overylay the graphs, we get the following picture.

If we set y = 0 we get the equation 0 = x + c. If we graph this equation for the previous values of c, we get a set of vertical lines parallel to the y axis ( x = 0 ).
If this equation is graphed in the xc plane we get a line through the origin (x = y). Look at the above graph; what can be conclustion can be made if you overlay the graph of x = y, and x = -y on the above graph?
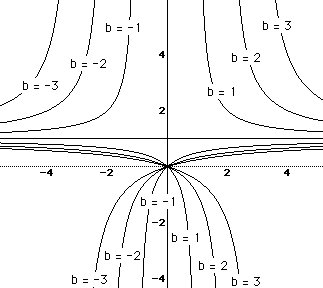
What if we set x = 0, we get the equation 0 = y + c. What do the different graphs of this equation look like? Again, what conclustions can be made?

In the following Example we will set xy = ax + y for a = -3, -2, -1, 0, 1, 2, 3, and we get the following picture.

Now, we will set xy = x + by for b = -3, -2, -1, 0, 1, 2, 3; and we get the following picture.


It might be helpful to look at the graphs of x - b = 0 and y - a = 0
The following graph is that of x - b = 0

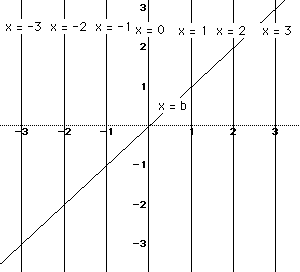
For the graph of y-a = 0 we get a similar picture, but of course we get horizontal intead of vertical lines, but the line y = a looks just like the line x = b.

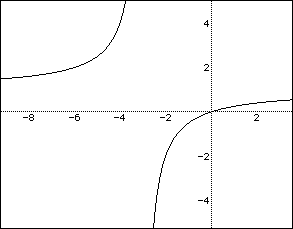
Now if we look at the graph of the equation (x- b)(y - a) = 0.

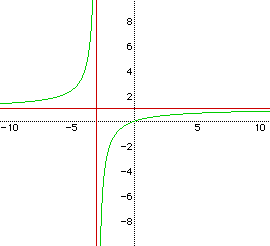
First we will look at the two equation (x-b)(y-1) = 0, and xy = x + by for b = -3, and we get the following picture.

The two staight lines is the graph of (x+3)(y-1) = 0. Review the graphs of x + 3 = 0,
and y - 1 = 0 to see how this graph is obtained. It appears that this equation forms the asymtopes for the equation xy = x - 3y (a = 1 and b = -3 as in the other equation).

It might be helpful to look at another picture overlaying these 2 equations with a different value for b to help us make conclusions. The following picture is obtained, if we set b=2.

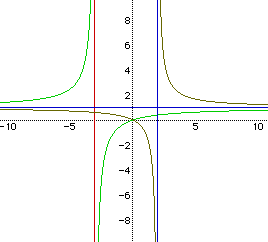
Again, it appears that we are getting the asymptopes.

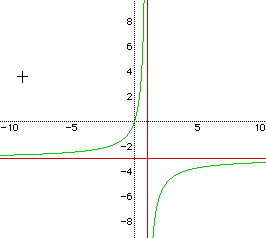
Now we will look at the two equation (x-1)(y-a) = 0, and xy = ax + y for a = -3, and we get the following picture.

Again, it appears that the equation (x- 1)(y+3) = 0 forms the asymtopes for the equation xy = -3x + y (a = -3 and b = 1 as in the other equation).
Therefore it looks like if we set both of these equations for the same values for a and b keeping c constant, we will get the asymptopes.

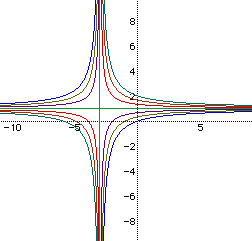
Now let us look at the graph of the equation (x - b)(y - a) = k (where k is any real number)
If we overlay the two graphs (x + 3)(y -1) = k and xy = x - 3y with k = -3, -2, -1, 0, 1, 2, 3, we get the following picture.

Look at the graphs in which c was varied at the beginning. This graph looks very similar.
Lets see if we can figure out what is going on.
If we take the equation (x - b)(y - a) = k, and multiply we get
xy = ax + by - ab + k.
Now if we compare this to our equation xy = ax + by + c we will get the same equation for c = -ab + k.

To check this we will look at the graph's for xy = x - 3y and (x+3)(y-1) = -3 and we get the following picture.

They are the same.

Return to Jennifer's Final Project Main Page