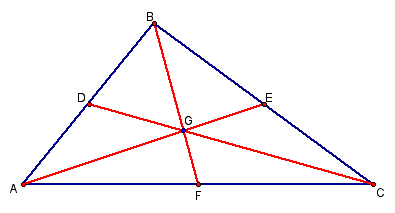
Prove: The medians of a triangle are concurrent.

Click here for a GSP 4.0 sketch to manipulate.

Given triangle ABC, show that medians AE, BF and CD are concurrent.

Since F is the midpoint of AC, AF = FC and

Similarly,

Thus,

By the converse of Ceva's theorem, medians AE, BF and CD are concurrent. The point where these medians intersect is known as the centroid.