

If we set a and b equal to zero and hold k constant at 1 and set t from -2 to 2 we get a graph that appears as
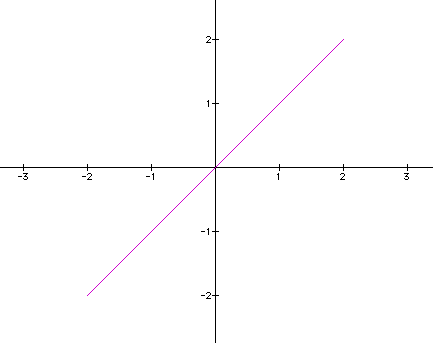
Some coordinates of the line are: (-2,-2) , (-1,-1) , ... ,(2,2). This would appear to be a slope of one.
This should be what we expected to see. If a and b are equal to zero our equations look like:
If we then change our k from one to four we get:
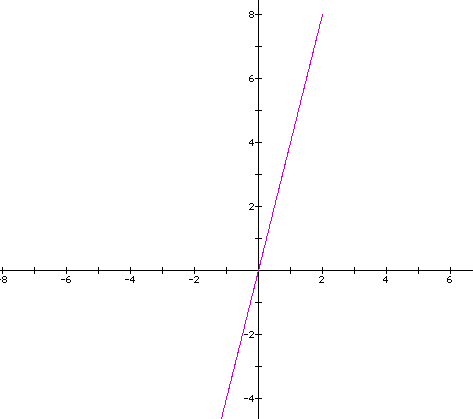
Some coodinates of the line are now: (-1,4) , (0,0) , (1,4) , and (2,8). This would suggest a slope of 4.
This furthers our point that k affects the slope of the line. As we have seen changing t would only extend our lines so we will now look at small values of t to show in the graphs.