Lets examine different variations with
. The equation when a and k are
set at one, and 
is set at -2 
to 2.
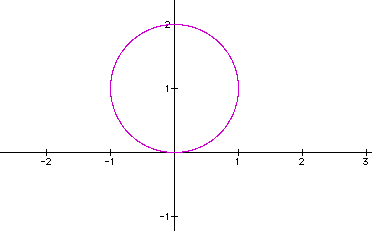
Now lets examine what happens when we vary a with the values (-2, -1, 1, and 2).
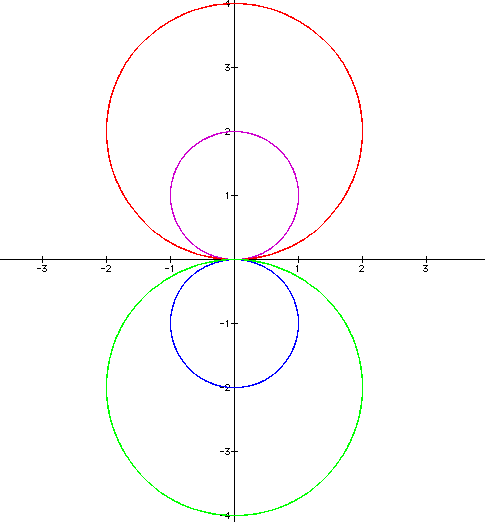
If we look at what has occured it seems that when a is changed to a larger number the curve gets larger in size and when a is changed to a negative it is reflected over y=0 (x-axis)
If we now look at what happens if we put a back to one and vary k with the values -3,-2,-1,1,2, and 3.
If we look at what changed when k was one and negative one, we see that the graph moved through a reflection over y=0. When k is two and negative two, a graph is produced that has four leaves and it does not seem to matter if it is positive or negative. When k is three and negative three however the leaves of the equations are different and have also reflected over y=0. This would leave one to believe that making k negatve would produce a reflection over y=0, however for even values the change would not be seen.