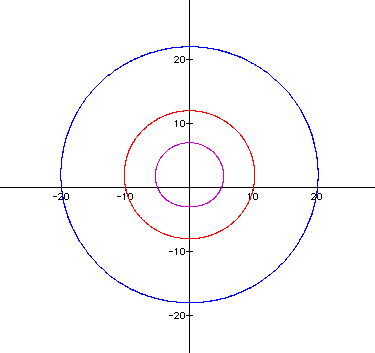
Lets examine different variations with
![]() . The equation when a, b, and k
are set at one, and
. The equation when a, b, and k
are set at one, and ![]() is set at -2
is set at -2 ![]() to 2
to 2![]() .
.
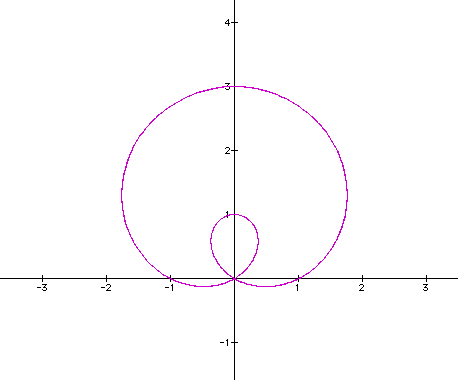
Now lets examine what happens when we vary a with the value 2 we get
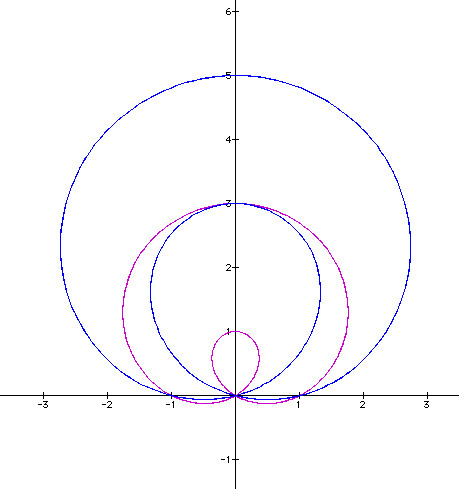
It would appeart that the outer curve has gotten larger, as we would assume from the previous applications, however the inside curve has gotten almost as large as the first curves outer curve. If we examine what occurs when we vary a to a negative value, the curve should reflect over the x-axis, based on the previous applications. (a=-1 and 1).
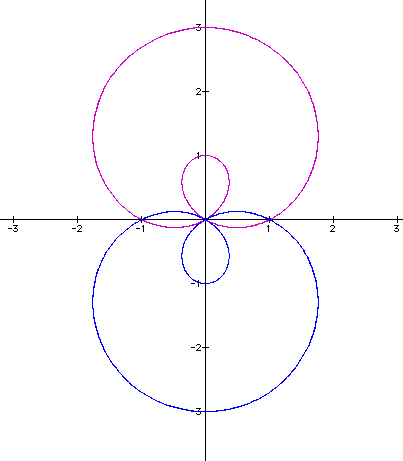
Changing a to a negative value seems to produce the same circle only reflected over the x-axis, as we had thought.
If we now look at what happens if we put a back to one and vary k with from 1 to 2, we get:
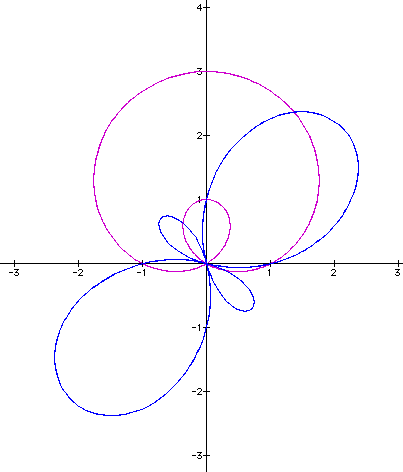
The graph appears to be multiplying in size as we would have also assumed from the previous applications. The larger curve seems to be spreading out more though and the inside curve also seems to spread out. If we examine what occurs if we go to k=3 we get
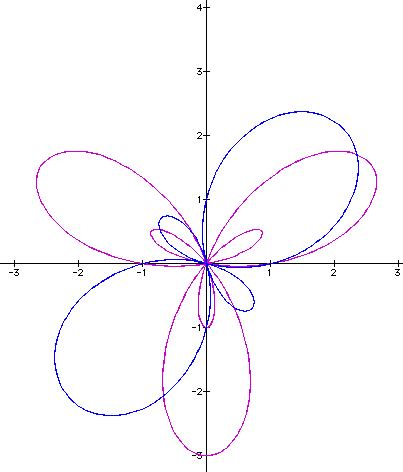
The curve seems to be doubling in its loops but also spreading out further. Now we can examine what happens if we move k to a negative number.
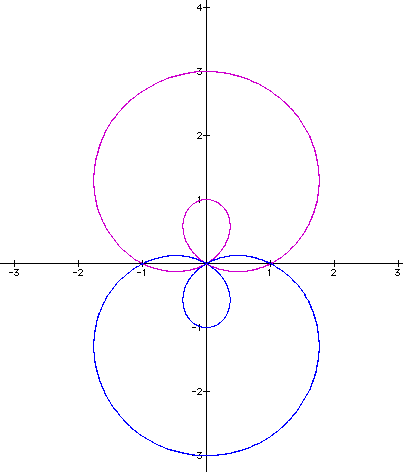
Moving k to a negative number also reflects the graph over the x-axis (expected from the previous applications). Now we just must examine if two is the same as the previous sin curve in that no change will be seen.
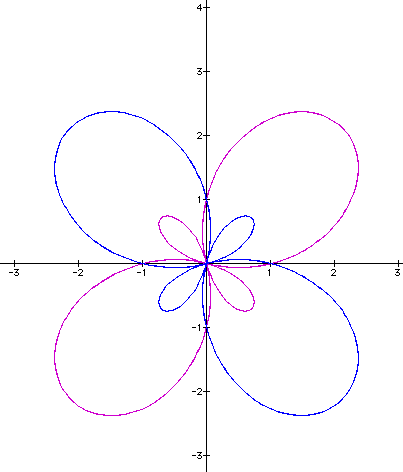
This is different from our previous applications because although the curves are reflecting over the x-axis because they are not in the same position, our leaves are formed and seen as the reflection. One could now assume that making k larger would produce thinner curves, with k number of leaves. Making k negative will produce a reflection over the x-axis.
The last examination must be of the b value. If we set a and k equal to one, and examine what occurs when b is equal to 1, 2, 3, -1, -2 , -3 we get
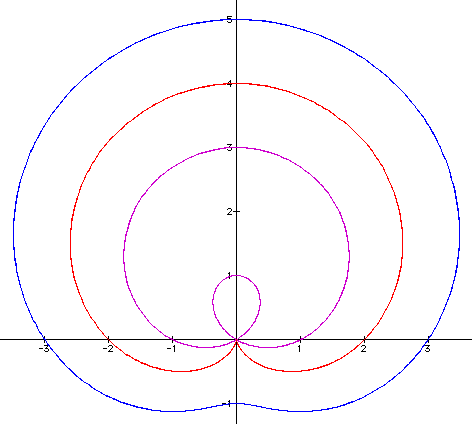
It would appear that changing the b value to a larger value produces a smoother curve and that changing b to a negative has no effect. If we continue to examine we find that b with a value of five produces a pretty smooth curve but when examining values of 10 and 20 the curve gets even smoother (and larger)