

Lets examine different variations with
![]() . The equation when a, b, and k
are set at one, and
. The equation when a, b, and k
are set at one, and![]() is set at -2
is set at -2 ![]() to 2
to 2![]() .
.
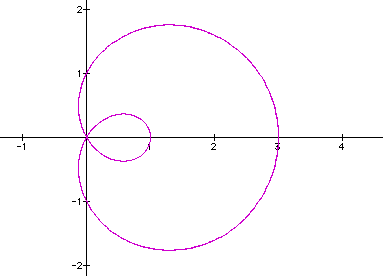
Now lets examine what happens when we vary a with the value 2 we get
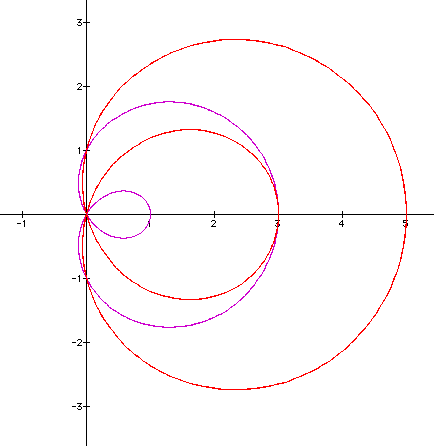
It would appeart that the outer curve has gotten larger, just as in the last exploration. If we examine what occurs when we vary a to a negative value, the curve should reflect over the x-axis, based on the previous applications. (a=-1 and 1).
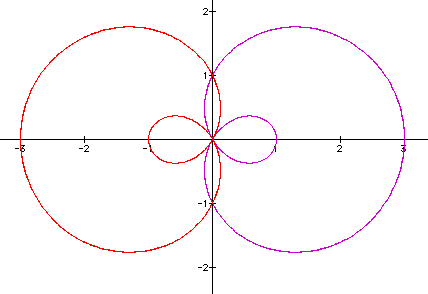
Changing a to a negative value seems to produce the same circle only reflected over the y-axis, as we should have expected from the previous explorations.
If we now look at what happens if we put a back to one and vary k with from 1 to 2, we get:
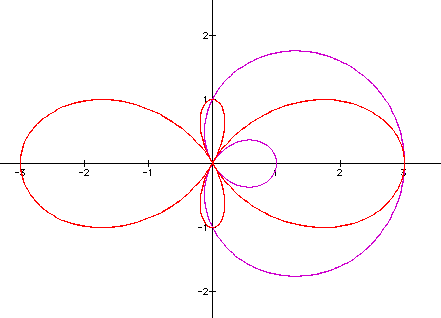
The graph appears to be multiplying in size as we would have also assumed from the previous applications. The leaves are multipling by the change in k and as k gets larger the leaves are getter more oval like.
Now we can examine what happens if we move k to a negative number. We will get the orginal curve, so it would appear that changing k in this case would have no effect on the curve.
The last examination must be of the b value. If we set a and k equal to one, and examine what occurs when b is equal to 1, 2, 3, -1, -2 , -3 we get
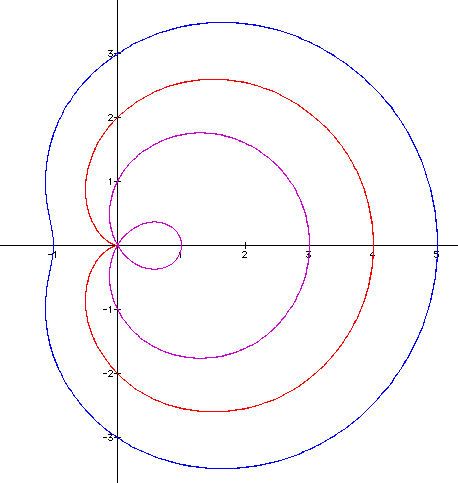
As in the previous application it would appear that changing the b value to a larger value produces a smoother curve and that changing b to a negative has no effect. The only difference is that the curve is on the side (x-axis), rather than on the y-axis.