Lets examine different variations with
. The equation when a, b, c, and
k are set at one, and 
is
set at -2
to 2.
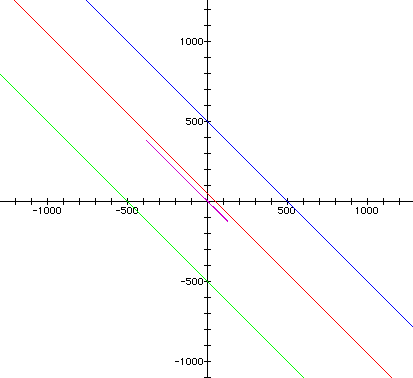
Now lets examine what happens when we vary a with the values 2 and 3 we get
It would appear that the line is shifting with the value of a. If we examine what occurs when we vary a to a negative value, the curve should reflect over the x-axis, based on the previous applications. (a=-1 and 1).
Changing a to a negative value seems to produce the same circle only reflected over the y-axis, which would imply what has typically occured when a was associated with cos.
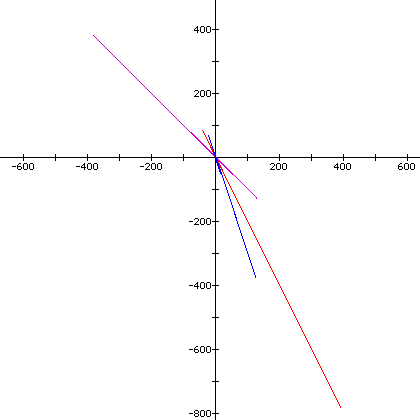
If we now look at what happens if we put a back to one and vary k with from 1 to 2, we get:
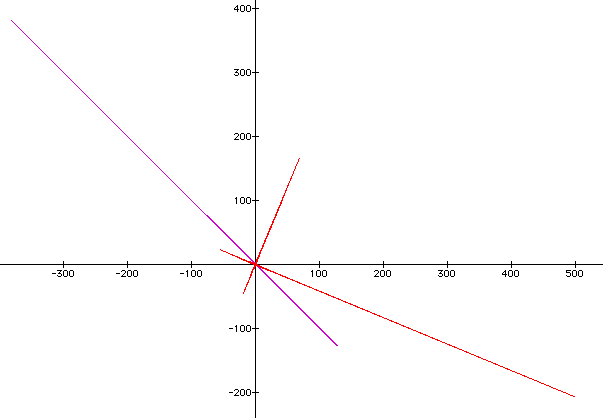
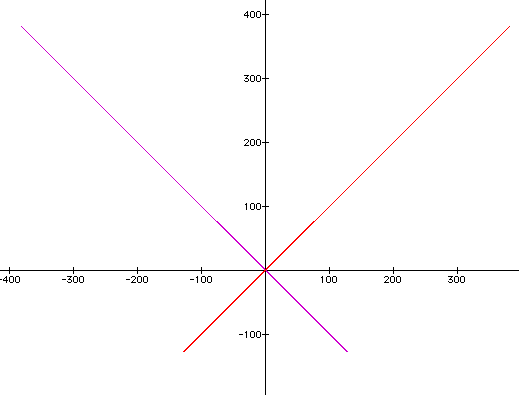
The graph appears to have doubled in the lines which would leave one to assume that as k increases the number of lines will also increase. If we move k to a negative number k=-1, we get
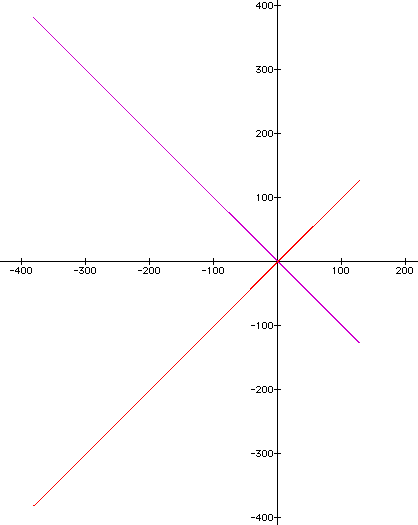
This appears to give an reflection of the graph over the y-axis.
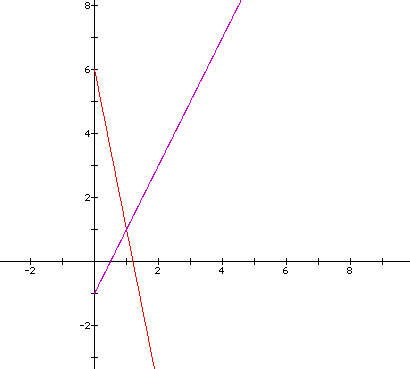
Now we need to look at what occurs when we look at b. If we look at what happens when b changes from 1 to 2:
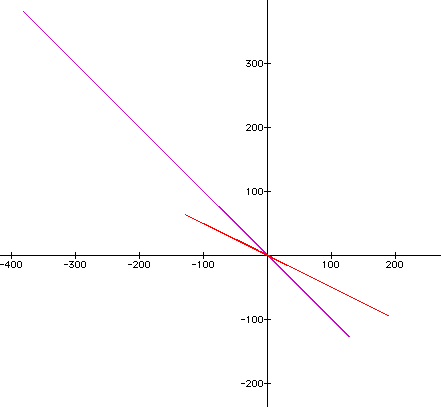
The line appears to be shortening and changing in slope. The line also appears to cross at a point after (0,0). Closer examination would imply the point is actually (1,0).
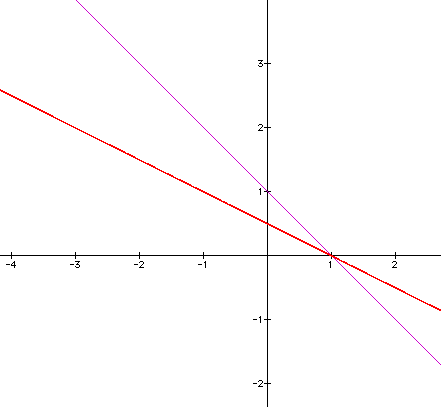
If we look at what happens when b is changed to a negative one we get:
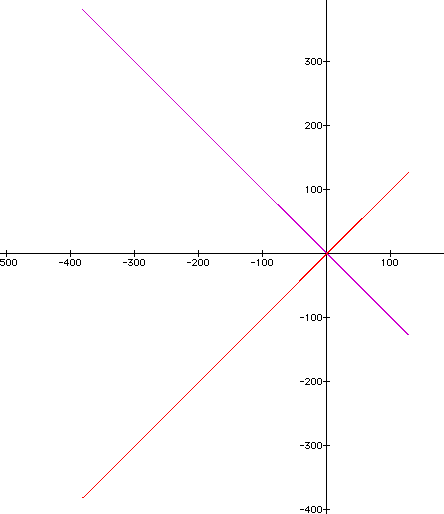
This would imply a reflection over the x-axis, which has been standard for making a the numeral in front of sin, negative.
The last examination must be of the c value. If we set c equal to 1, 2, -1, -2 we get
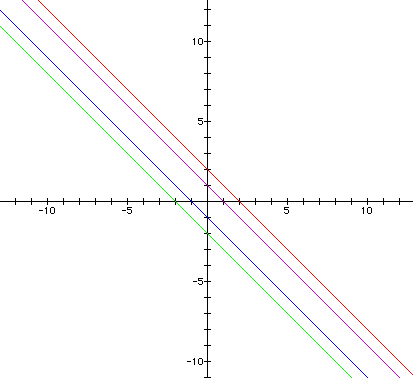
It appears when examined closely this moves the line. When looked at from a far distance to see the entire line, the numbers are too close to see differences. Therefore if we look at the c values of say 1, 50, 500, and -500, we get something that appears as:
