

If we move the circle B to a circle on circle A.
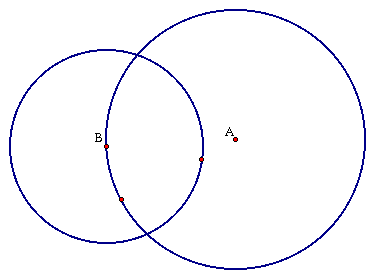
Let's not use our script and create the tangent circle from scratch. First we need to pick a point C on circle A.
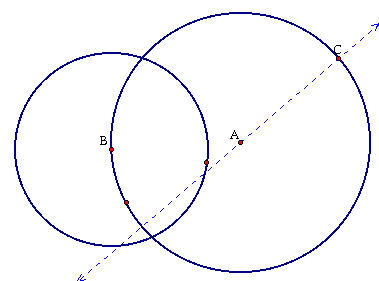
Next lets construct circle C with the same radius as circle B, and then select point D that is an intersection of circle C and line AC.
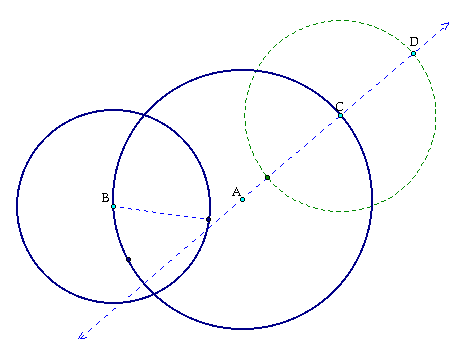
Next let us connect point D to point B and form segment DB. Then finding the midpoint of DB gives us point E.
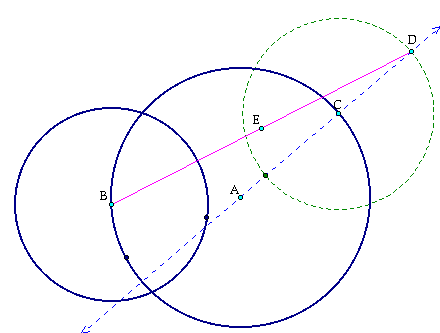
Now let us draw a perpindicular from E and call the intersection of the perpindicular with line AC, F.
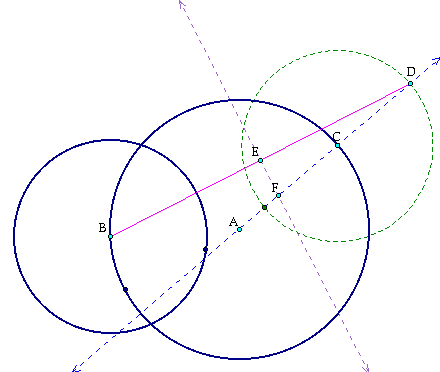
The segment FC with the center at point F constructs the radius of a circle F that is tangent to both circle A and circle B. What ends up is the following:
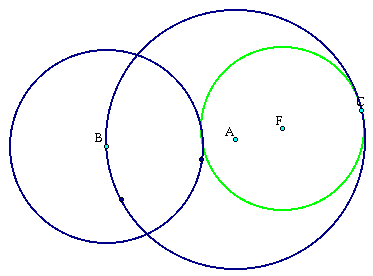
The locus of this would like this:

With the segments included a presentation like this would occur:
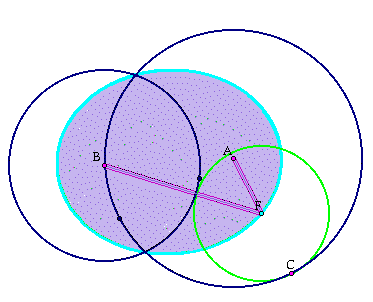
Click here to investigate these circles further