It's a pretty weird story to how this quadratic came to be. I came up with this through one of my homework questions in precalculus when I was in high school. I was given and was asked for the root and some other stuff. For some reason, unknown to me now, I found this equation interesting.

I desided to generalize this equation because each constant had a factor of 3 and the middle constant is the difference of the first from the last plus the last is the square of the first. Because of all this I was able to put the constant term into a single variable. Initially I had the equation but have changed the a's to n's so that i could examine it in Graphing Calculator. When I graphed this equation in Graphing Calculator I found something very interesting going on. When the n changes the vertex of the set of quadratics seemed to trace a cubic. I though I had done something wrong at first because how can a set of quadratics define a cubic.

To my amazement I was right, this does define a cubic. Check it out. (This may take a few minutes it's pretty big)

Let's change this equation a little bit an see what happens.

All that I changed is the b term, replacing the second n with a 1, to see what happens when that part is constant.

Check it out (This may take a few minutes it's pretty big)

It looks very similiar to the other graph but it is a little different and this becomes very evident when you try solving of the vertex. The first part is easy, find x.

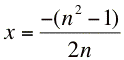
and substituting that into the original equation for x you get

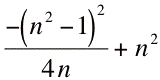
So the vertex follows

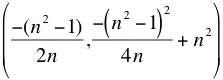
Now solving for n to come up with an equation (like what was done above) gives you problems, you get

n has to be both the postive and negative values for the equation to work, so it is not possible for us to come up with only one equation.

This movie shows the graph of the positive value of x in red and the negative value of x is in blue.

Check it out (This may take a few minutes it's pretty big)

Pretty crazy huh?

Now lets investage this stuff a little further. What about the equation ?

This is almost the same as the original equation, I have just removed the n from the beginning. When I did this I didn't think it would make to much of a difference, probably just change the equation of the cubic that you get from tracing the vertex. I was way off.
Check this one out (This may take a few minutes it's pretty big)

Now this one gets weird. I tried solving for the equation of the vertex in terms of n just like I did in the previous quadratic and I got that the vertex is 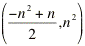. This is clearly not a function but you can come up with a equation in terms of x

So, just like before n has both a positive and a negative value.

This movie shows the graph of the positive value of x in red and the negative value of x in blue.

Check it out (This may take a few minutes it's pretty big)

Let's check out one more. What about the equaton ?

The only difference to this one from the original is I multipled the b term by .

The vertex turns out to be

The y-coordinate is a 6th power polynomial.

Check this one out (This may take a few minutes it's pretty big)

As you can see it's not a function either, there's some overlap when around x = 1

I tried graphing this one as a parametric equation, setting x equal to the x-coordinate of the vertex and y equal to the y-coordinate of the vertex. This graph is pretty neat.

Check it out (part 2) (This may take a few minutes it's pretty big)

Now there needs to be more investagation and some proof but my hypothesis is that the original quadratic is the only one that you can deduce a cubic from.