Given a triangle ABC, prove that the three altitudes are concurrent (meet at one point).

To prove this theorem, I will be using Ceva's theorem:

In a triangle ACE, three lines AD, BE and CF intersect at a single point K if and only if
AB/BC· CD/DE· EF/FA = 1

 Note: This is a special case of Ceva's theorem where the point K is the orthocenter, H. To see the proof of the general case see my final assignment link on my main page.

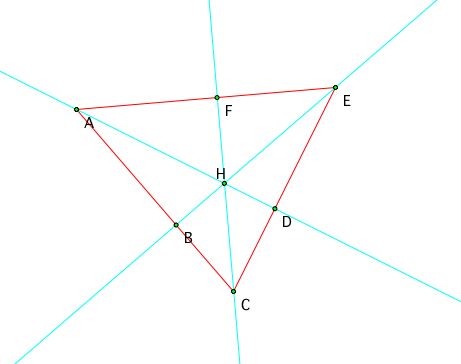
Given triangle ACE, let's first look at the areas of triangles AHF and EHF.

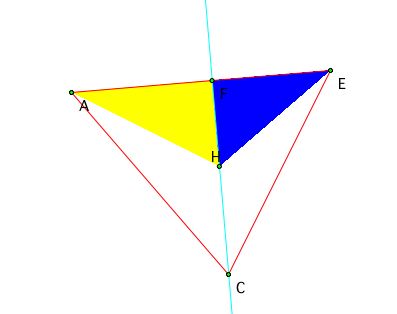
Area of triangle AHF =1/2 * (AF)(FH)

Area of triangle EHF = 1/2*(FE)(FH)

By dividing the areas of the two triangles you get:

(Area of triangle AHF)/(Area of triangle EHF)= (AF)(FE)

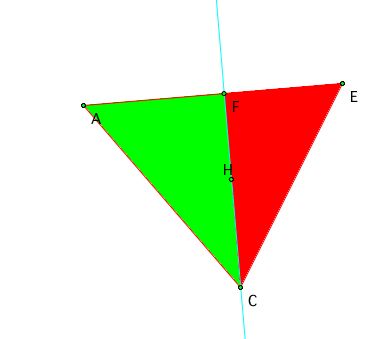
Notice that is triangle has the same bases as the one above, AF and FE

So, by dividing the areas like above you get:

(Area of triangle ACF)/(Area of triangle ECF) = (AF)/(FE)

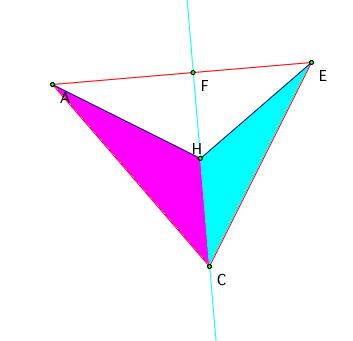
Then it is easy to see that the ratio of the remaining areas must hold the same equality

(Area of triangle ACH)/(Area of triangle ECH) = (Area of triangle ACF)/(Area of triangle ECF) = (Area of triangle AHF)/(Area of triangle EHF) = (AF)/(FE)

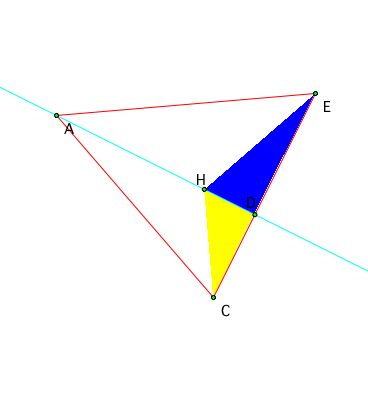
Now looking at the triangle from the perspective of altitude AD and the same procedures as above you get that

(CD)/(DE) = (Area of triangle ACH)/ (Area of triangle AEH)

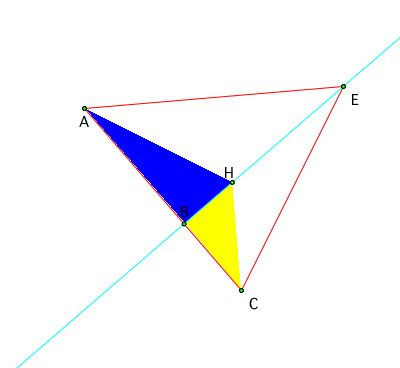
Looking at the triangle from the purspective of altitude BE you get

(AB)/(BC) = (Area of triangle AEH) / (Area of triangle CEH)

To figure out that AB/BC· CD/DE· EF/FA is all that is needed is some substitution of areas to get:

(Area of triangle AEH) / (Area of triangle CEH) * (Area of triangle ACH)/ (Area of triangle AEH)* (Area of triangle ECH)/ (Area of triangle ACH) = 1

So by Ceva's thereom you can conclude that all three altittudes are concurrent.