EMAT 3500 Assignment 13


For each of the following items, use a graphing program, such as Graphing Calculator 3.1, to explore, understand, and extend. I would like you investigate any five of the following problems... pleae create a file that shows you have done so. In that file you should answer one or two questions that are either posed here on this problem set or that you create yourself. One to two graphs will suffice as support

Then choose one problem that you would like to explore more in depth. Write-up this more detailed investigation and post it to your webpage as Assignment 13. Be creative, be inquisitive, be mathematical, and have fun.



1. Examine:

.

See the graph.What happens if the 4 is replaced by other numbers (not necessarily integers)? Try 5, 3, 2, 1, 1.1, 0.9, -3. Any unusual event? Interpret.

What equation would give the following graph:

What happens if a constant is added to one side of the equation? Try several graphs in some systematic way. Click here for one set of graphs.

Try graphing

See Graph.

Click HERE to open Graphing Calculator 3.1 to explore this equation.



2. Make up linear functions f(x) and g(x). Explore, with diffefent pairs of f(x) and g(x) the graphs for

Summarize and illustrate.



3. Find two linear functions f(x) and g(x) such that their product

is tangent to each of f(x) and g(x) at two distinct points. Discuss and illustrate the method and the results.

 

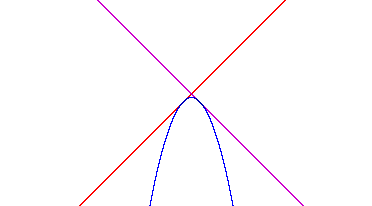
Do you want to see someone else's discussion of this? If so click here.



4. Repeat Problem # 3 above where f(x) and g(x) are quadratic functions and each function, f(x) and g(x) is tangent to h(x) in two different points. That is, h(x) is a fourth degree equation and each of the second degree equations, f(x) and g(x) is tangent to h(x) in two points.



5. Examine graphs of

y = a sin(bx + c)

for different values of a, b, and c.



6. Graph

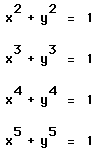
What do you expect for the graph of

or



7. Let f(x) = a sin(bx + c) and g(x) = a cos(bx + c).

For selected values of a, b, and c, graph and explore:

 



8. Explore the following equation for different values of a.

 



Some examples:

| a = 0 | | a = 1 | | a = 3 | | a = 5 | | a = 10 |

| a = -10 | | a = -3 | | a = -5 | | a = .10 |

| a = .50 | | a = -.50 | | a = -.10 |

| Multiple Graphs |



9. Consider two points (3,4) and (-5,-2). For any point (x,y) we can write the distance equations for these as


Explore graphs with these two distance equations. For example,

a. Consider when each is set to a non-zero constant. Circles are graphed.

b. Consider the sum

for various values of C.

c. Consider the product

for various values of C.

d. Other?

More about Lemniscates


Return to EMAT 6680 Home Page.