This Assignment has a set of activities
to help become even more familiar with GSP and to review some
basic geometry in the context of triangle centers. Please construct
and investigate each of the following activities. Write-up a two-three
sentence description of what you notice in numbers 1 - 4. Number
five is where the real fun is :) Complete that construction and
then write a one-two paragraph description about what you notice
- comparing the centers not just to the original triangle but
also to each other.
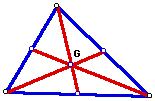
1.
The CENTROID
(G) of a triangle
is the common intersection of the three medians. A median of a
triangle is the segment from a vertex to the midpoint of the opposite
side.
Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.

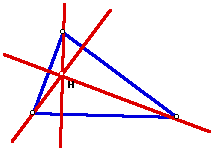
2. The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes.
Use GSP to construct an orthocenter H and explore its location for various shapes of triangles. (Make sure your construction holds for obtuse triangles.)
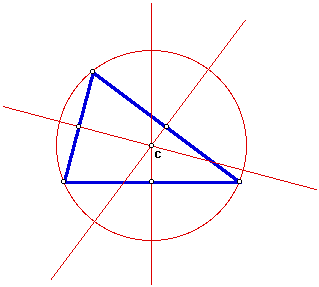
3.
The CIRCUMCENTER
(C) of a triangle
is the point in the plane equidistant from the three vertices
of the triangle. Since a point equidistant from two points lies
on the perpendicular bisector of the segment determined by the
two points, C is on the perpendicular bisector of each side of
the triangle. Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
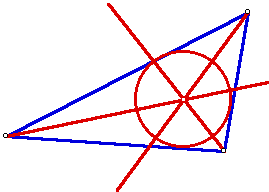
4.
The INCENTER
(I) of a triangle
is the point on the interior of the triangle that is equidistant
from the three sides. Since a point interior to an angle that
is equidistant from the two sides of the angle lies on the angle
bisector, then I must be on the angle bisector of each angle of
the triangle.
Use GSP to find a construction of the incenter I and explore its locationfor various shapes of triangles. The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle.
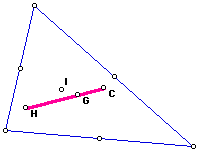
5.
Use GSP to construct G, H, C, and I for the same triangle. What
relationships can you find among G, H, C, and I or subsets of
them? Explore for many shapes of triangles.
How to Turn in and Label your Work
You will need to e-mail me your gsp file including your write-up. Please use the document options command on GSP to add blank pages to your file. Thus you will have five tabs at the bottom of your GSP sketch... one for each construction. Again, please label your file as follows...
GSP File: your last
name and first initial_gsp2.gsp
For example, I would e-mail myself (at lsheehy@ngcsu.edu) the following file:
sheehyl_gsp2.gsp
Note!! Please label the Subject exactly as follows: gsp2