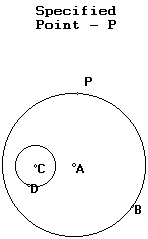
GSP, or Geometer's Sketchpad, is a tool in understanding geometric relations. GSP gives us a way to experiment with the geometric relations. The geometric relation I will explore is that of a circle tangent to two given circles.
Problem: Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with the one point of tangency being the designated point.
First we will use GSP to create a picture of the problem:

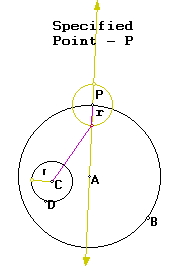
We know the circle tangent to the large circle at point p will have its center on a line through A and P so we can use GSP to draw it:
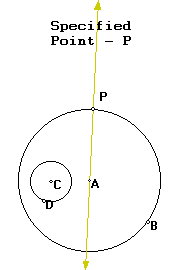
We also know that the radius of the tangent circle plus the radius of the circle defined by CD will give us the distance from the center of the tangent circle and CD. We know that the bisector of the vertex angle of an isoceles triangle is median to its base. We know that the center of our tangent circle will be the vertex of an isoceles triangle with the base being a segment from C to a point a distance r from P. I can construct this with GSP:
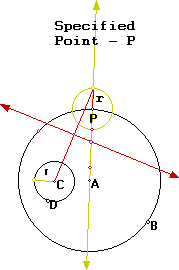
I then can find the vertex of the isoceles triangle by constructing a line perpendicular to the base at the median of the base, thus finding the center of my tangent circle:
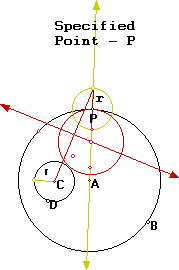
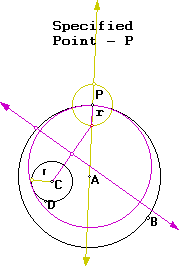
I can find another tangent circle at point P by making the base of the isoceles triangle as follows:
By finishing the construction for my isoceles triangle I get :
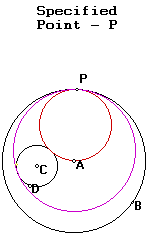
Let's look at just the circles:
We can find the locus of the centers of the tangent circles as point P is moved around the circle AB.
We get:
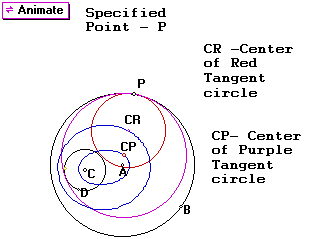
As you can see a conjecture that results from looking at the picture is that the locus of centers are ellipses with foci at A and C , the centers of my original circles.
Now we can change the two original circles so the specified point P of tangency is on the smaller circle:
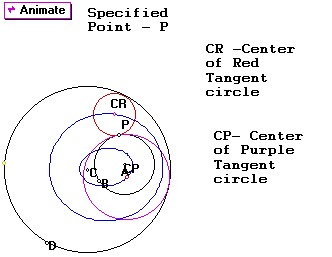
We see that the locus of centers of the tangent circles still appears to be ellipses with A and C, the centers of the given circles as foci. Next We can move the smaller given circle outside the larger given circle and watch what happens to our locus. Click below to see a GSP sketch. You can move the objects around.
As you see when the smaller given circle with the specified point of tangency was external to the larger circle it appears the locus of centers of tangent circles was a hyperbola with the centers of the given circles as foci.
To prove these conjectures we might use the definitions of ellipses and hyperbolas and look at the constructions of the tangent circles to prove our conjectures.