To Kastner, the Analyst, it appeared that the application of algebra to geometry would free the student from the stern discipline of Euclid. It would enable him to think for himself instead of having to watch the lips of his teacher. One of Kastner's sentences could fitly be inscribed over the door of any modern school : "The greatest satisfaction that we know is to find the truth for ourselves."

J. L. Synge

Exploring Polynomials and Volume Using Multiple Approaches

The following investigation explores an application of a polynomial that arises from volume. The investigation will explore this relationship using several different approaches:

Algebra Xpresser
GSP
Excel.
Consider the following problem:

Algebra Xpresser Approach


Using Algebra Xpresser, this problem can be explored rather easily.

The volume of the rectangular box is the product of the dimensions V=lwh. When the cardboard is folded up, the dimensions of the box in inches will be (25 - 2x) long by (15 - 2x) wide by x high.
So,

V=(25 - 2x)(15 - 2x)(x) cubic inches.


Consider the graph of the polynomial V=(25 - 2x)(15 - 2x)(x). Since the dimensions of the box cannot be negative, consider only positive values for x. One other consideration to take into account is the maximum value that x can be. Since the width of the box is (15 - 2x) inches and the width cannot be negative, consider what values will make the expression 15 - 2x > 0. Solving this algebraically, x cannot exceed 7.5 inches. So, x<7.5. The graph will express volume in terms of the size of the box where 0<x<7.5.


size of cut out square

It is important to point out to the students since volume is 3-dimensional, they should expect a volume formula to involve a degree of three. Hence, the graph will have 2 turning points. It would be nice, however, to show the students the behavior of the full graph for x<0 and x>7.5. The discussion at hand, however, will focus only on 0<x<7.5. Consider the full graph and its behavior.

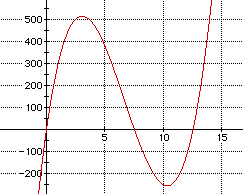
Getting back to our exploration at hand, consider once again the graph of

V=(25 - 2x)(15 - 2x)(x).


size of cut out square

The graph shows the maximum volume occurs somewhere around x=3. We want to find a closer estimate which can be done by magnifying the peak of the graph.

The graph suggests the Maximum Volume of the box is 513 cubic inches and occurs when the size of the cut out square box is 3.03 inches.

The question still remains what size of the square would produce a box of volume equal to 400 cubic inches or V=400. This information can also be obtained by considering the graph


size of cut out square

and exploring when V=400, what value must x be. The graph shows when x is approximately equal to 1.7, the volume is also equal to 400. This estimate can be more carefully considered by magnifying that particular region of the graph.


size of cut out square

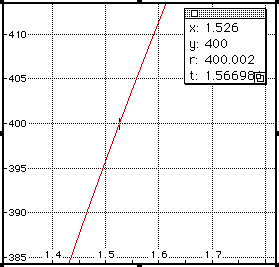
With magnification, the graph clearly suggests when x=1.526, V=400. So when the size of the cut out square box is 1.526 inches, the volume of the box will be 400 cubic inches.

Using Algebra Xpresser shows students the solutions graphically. It is a powerful means to reveal to students that polynomials have graphs and behave in particular way and that behavior has real-world applications such as this particular cardboard box problem. This problem could easily be taught using only algebraic(symbolic) manipulation which is an important aspect to this problem. However, often students only see one way to work a problem. Students need contact studying algebraic concepts from multiple perspectives: numerically, symbolically, and graphically. This demonstration provides another alternative for answering the problem from a graphic orientation.

GSP APPROACH

GSP provides another perspective to the problem at hand.

Click here for an animation that shows what happens to the rectangular cardboard box as the size of the cut out square box increases and decreases.

What did you notice?

As thecut out square piece increases in size, there will come a point when you would no longer have a box. This occurs when x=.75 inches which is the same as x=7.5 inches. Recall, that was the same maximum value for x as in the Algebra Xpresser demonstration. So, the square box cannot ever exceed 7.5 inches. Otherwise, the rectangular box would not exist.

GSP provides students with a visual experience of the changes that occur with the box as the size of the cut out square changes in size. Students see firsthand the changes that take place with the box as if they were cutting out the pieces themselves.

Spreadsheet Approach Using Excel

Using a spreadsheet format, such as Excel, provides the students with an experience that is more numerically based. Here the first spreadsheet shows the sizes of the cut out squares and their corresponding volumes. The volume formula needed for computation is the same as in the previous approaches V=(25-2x)(15-2x)(x). Except in the spreadsheet format, the x must be replaced with the appropriate cells for proper calculation.

Spreadsheet 1

Several important items to consider are when the highest volume occurs and what the negative values for the volume imply. First, volume cannot be measured in negative units. Thus, it does not make sense to consider when x>7.5 as previously discussed in the earlier approaches.

Next, the maximum volume occurs when x is approximately equal to 3. We are not quite sure how accurate this is, so we can investigate closer estimates by narrowing in on the values near 3. The maximum volume must occur somewhere between 3<x<3.5. Therefore, consider values between 3 and 3.5 using the spreadsheet. Instead of increasing x by increments of 0.1, the approach will be to increase x by increments of 0.01 to zero in on the maximum volume.

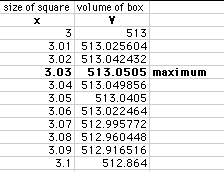
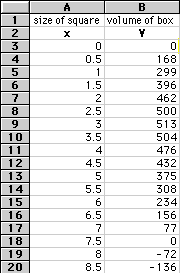
The spreadsheet clearly shows the maximum volume is 513.05 cubic inches and occurs when the size of the cut out square is 3.03 inches. This clearly matches the maximum volume obtained in the Algebra Xpresser approach. This method actually seems to provide even more accuracy.

What size of the square will produce a box of volume=400 cubic inches?

Using spreadsheet 1, the volume of the box will be equal to 40 cubic inches when x is somewhere between 4.5 and 5 inches.

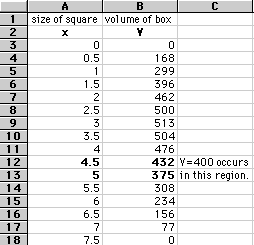
To discover when V=400, increase 4.5 by increments 0.001 to obtain the correct value for x.

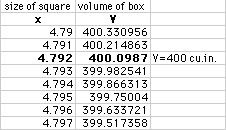
The volume of the box will be equal to 400 cubic inches when the cut out square box is 4.792 inches. If you are not satisfied with this estimate, consider making increments even smaller where x is being increased by increments of 0.00001.

A closer estimate for V=400 is when x=4.79284.

The spreadsheet does provide a graphic utility. The following is a graph representing the volume of the box for various sizes of x.

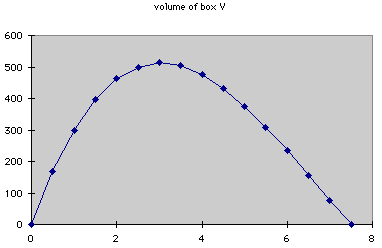
The graph, however, cannot be easily magnified and changed as with Algebra Xpresser.

The advantage of using Excel is its capability to perform rapid data calculations.

Excel provides an opportunity to explore the cardboard box problem from a numerical approach. Algebra Xpresser provides a graphic approach. GSP provides a visual experience.

Return to Final Project Page