Assignment 14
Euclidean Constructions using Straightedge and Compass
Alone at nights,
I read my Bible more and Euclid less.
Robert Buchanan (1841-1901)
(An Old Dominie's Story)
| Problem 1 |
Which constructions in GSP can be done using only the three Euclidean construction rules?
More precisely, for which of the items in the "Construction" menu can a script be written using only the items
"Line" (or "Ray" or "Segment")
"Circle by Center + Point"
"Point at Intersection"?
If it's not possible, explain why.
Point on Object
It is impossible to construct a point on an object using the three Euclidean constructions above. It could be done if you were considering the point on object to be a point at intersection. However, simply picking an arbitrary point to construct on an oject cannot be done.
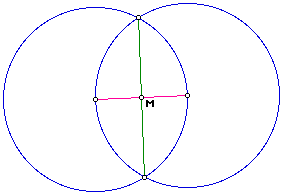
Point at Midpoint
Point at Midpoint is possible to construct using only the Euclidean rules above.

Click here for a GSP Script.
Why does this construction work?
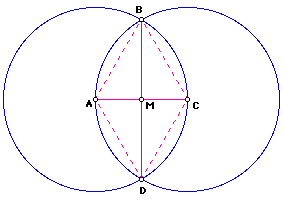
Segments AB, BC, CD, AD are all congruent, since they are all radii of the circles A and C whose radii are equal by construction. BD is a shared side. Therefore, triangles ABD and CBD are congruent, by SSS. Then, by SAS, triangle ABM is congruent to triangle CBM. Since corresponding parts of congruent triangles are congruent, segment AM is congruent to segment CM. Hence, by definition of midpoint, M is the midpoint of segment AC.
Perpendicular Line
It is possible to construct a perpendicular line using the three Euclidean rules above.
Special Case: Perpendicular Bisector
(This case follows directly from above. This case is also a special case of Case II below.)
In the following picture, line j is perpendicular to line k.
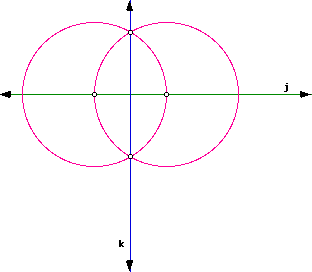
Click here for a GSP script.
Why does this construction work?
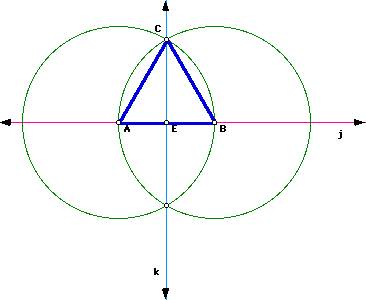
Segments AC, BC and AB are congruent to each other, since they are all radii of circle A and circle B. Also, since segments AC, BC and AB are congruent to each other, triangle ABC is equilateral. Therefore, each angle measures 60 degrees, angle A, angle B, and angle C. Since line CE bisects angle ACB, angle ECB measures 30 degrees. We know angle EBC measures 60 degrees, ECB measures 30 degrees, thus, angle CEB must measure 90 degrees. Therefore, by definition of perpendicular lines, line j is perpendicular to line k.
Following on the same argument above for the midpoint, we know that triangle ACE is congruent to triangle BCE (see above). Therefore, by corresponding parts of congruent triangles, angle AEC is congruent to angle BEC. Since angle AEC and angle BEC form a linear pair and the angles are congruent to one another, it follows that angle AEC and angle BEC measure 90 degrees. Therefore, by definition of perpendicular, line AB is perpendicular to line EC.
Case I: Construct the perpendicular to a given line and a point not on the line.
Here line j is perpendicular to line m.
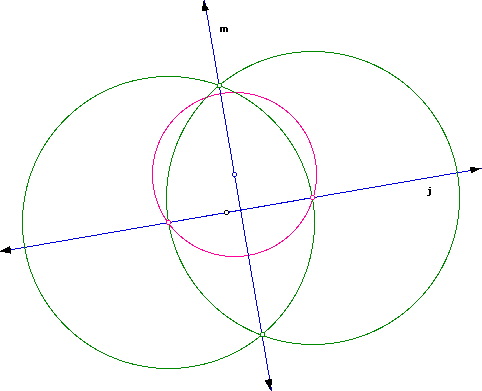
Click here for a GSP script.
Why does this construction work?
The reasoning process is the same as above for the midpoint of a segment and perpendicular bisector. See above for explicit reasons.
Case II: Construct the perpendicular to a given line and a point on the line.
We bgein with line j and the point A that lies on line j. We are able to construct the perpendicular line k, through A, to line j.
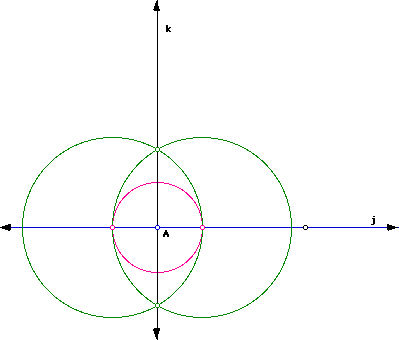
Click here for a GSP Script.
Why does this construction work?
The reasoning process is the same as above for the midpoint of a segment and perpendicular bisector. See above for explicit reasons.
Parallel Line
It is possible to construct the parallel to a given line and a point not on the line using the three Euclidean rules as stated above.
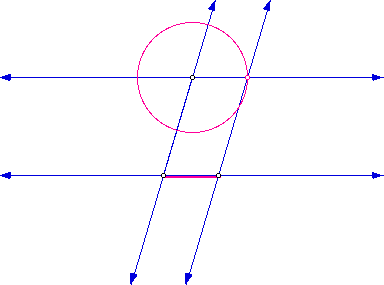
Here line j is parallel to line k.
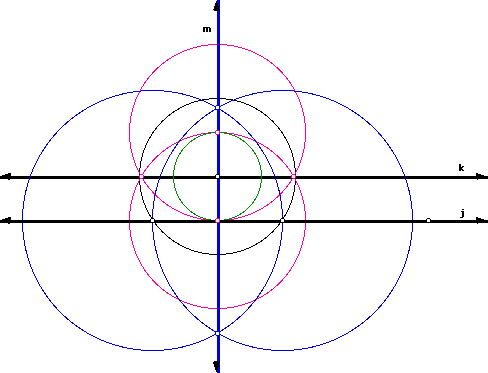
Click here for a GSP script.
Why does this construction work?
Based on the past explanations of why the preceeding constructions work, we constructed line m perpendicular to line j and then line k perpendicular to line m. If two coplanar lines j and k are perpendicular to the same line, then they are parallel to each other. Therefore, we can say that line k is parallel to line j, based on this theorem. This theorem directly follows from the Corresponding Angles Postulate that says, Suppose two coplanar lines are cut by a transversal and if two corresponding angles have the same measure, then the lines are parallel. In the figure above, line m is a transversal and the corresponding angles both measure 90 degrees, since the lines were perpendicular to each other.
Angle Bisector
It is possible to construct the angle bisector using the three Euclidean construction rules as stated above.
Here ray BF is the angle bisector of angle ABC.
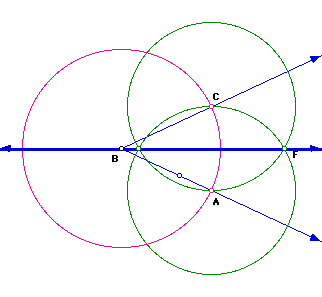
Click here for a GSP script.
Why does this construction work?
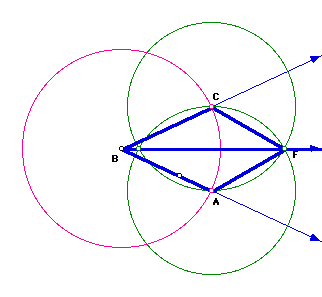
Since segment BC and AB are radii of circle B, then segment BC is congruent to segment AB. Similarly, segment CF is congruent to segment AF. Segment BF is congruent to BF, since it is a common side of the triangles BCF and BAF. By SSS, triangles BCF and BAF are similar. Since corresponding parts of congruent triangles are congruent, angle CBF is congruent to angle ABF. By the definition of angle bisector, ray BF is an angle bisector of angle CBF.
Circle by Center and Radius
This construction is possible using the three Euclidean construction rules.
Click here for a GSP Script.
Why does this construction work?
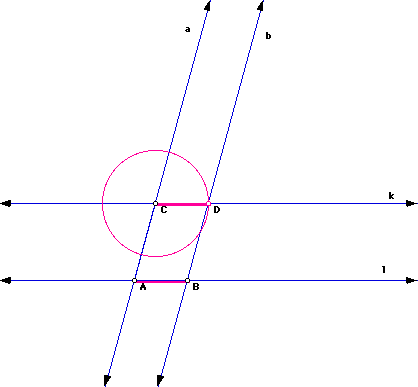
Since line l is parallel to line k and line a is parallel to line b, ABCD is a parallelogram, by definition. Therefore, segment AB is congruent to segment CD, since opposite sides of a parallelogram are equal.
Arc on Circle
This construction is possible using the three Euclidean construction rules.
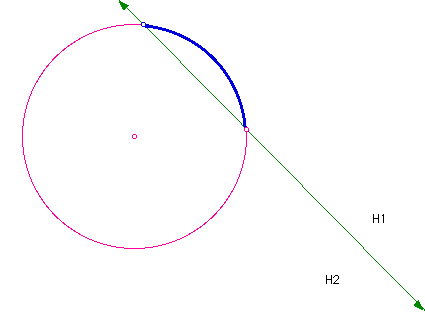
Click here for a GSP Script.
With this script, I had to use the arc on circle to define the arc for illustrative purposes. But, intuitively, you should see that the arc is all of the points between the two points that make the line that determines the half-planes, H1 and H2. (see further explanation below)
Why does this construction work?
Consider two points on the circle and the line determined by those two points. Suppose the line determines the half-planes, H1 and H2. Then we can construct the arc on the circle as being all of the points, on the circle, in the half-plane, say H1, between the two points on the line that determined the half-planes, H1 and H2.
Arc Through Three Points
This construction is possible using the three Euclidean construction rules.
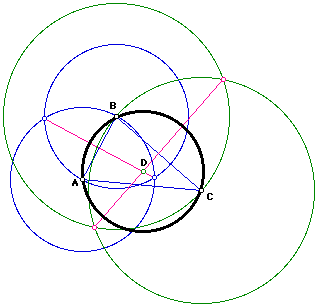
Notice, we had to first draw the circle D which contains the three points A, B, C. The arc going through points A, B, C is inherent in the circle D. If we want, we can now erase arc AC and are left with arc ABC.
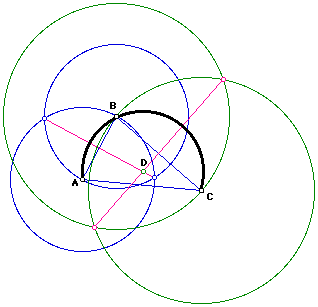
Click here for a GSP script.
Why does this construction work?
We began with three points A, B, C which formed the triangle ABC. Then we constructed the circumcircle of triangle ABC. Point D is the circumcenter of the circumscribed circle for the triangle ABC. By definition of circumcircle, the segments DA, DB, and DC are radii of circle D, and thus are congruent to each other. Furthermore, it is obvious that we can draw an arc through the points A, B, C which are contained in circle D.
We can also think of segment (line) AC as determining two half-planes, H1 and H2, where point B is in H1. Thus, we can think of arc ABC as all of the points lying in H1 and the two half-planes are determined by the line going through the two points, A and B.
Locus
This construction is impossible using the three Euclidean construction rules.
Intuitively, we cannot construct a path that an object is to travel on using the three Euclidean rules.
Interior
This construction is possible using the three Euclidean construction rules.
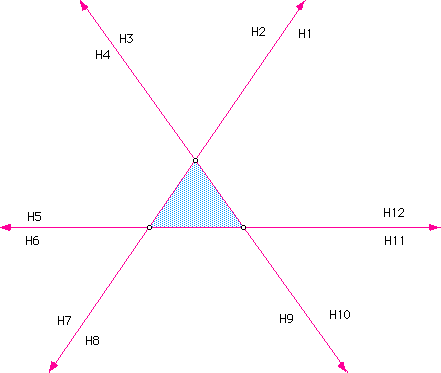
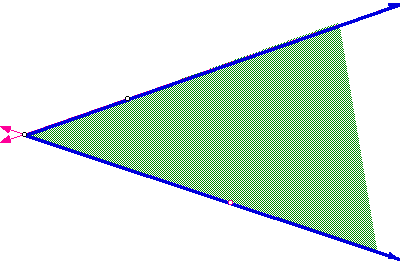
Why does this construction work?
The interior of a polygon, such as the above triangle, and an angle can be thought of as the intersection of all of the half-planes, determined by the sides of the polygon or the rays of an angle; that is, all of the points that lie in the intersection of those half-planes.
The interior of a circle can be thought of as all of the points that are less than distance of the radius; that is, if P is a point in the interior of a circle A, then AP < r.
| Problem 2 |
Do the following constructions using the three Euclidean construction rules plus any GSP construction rules which you showed in problem 1 are obtainable from the three Euclidean rules.
Part A
Given two points, construct an equilateral triangle with the two points as vertices.
This construction process parallels the steps involved in constructing a midpoint on a segment and also a perpendicular bisector.

Click here for a GSP Script that will construct an equilateral triangle given the two points as vertices.
Why does this construction work?
Segments AC, BC and AB are congruent to each other, since they are all radii of circle A and circle B and the circles A and B have the same radius. Since segments AC, BC and AB are congruent to each other, triangle ABC is equilateral, by definition of equilateral.
Part B
Given two points, construct a square with the two points as adjacent vertices.
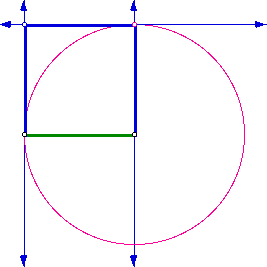
Click here for a GSP Script that will construct a square given two points as adjacent vertices.
Why does this construction work?
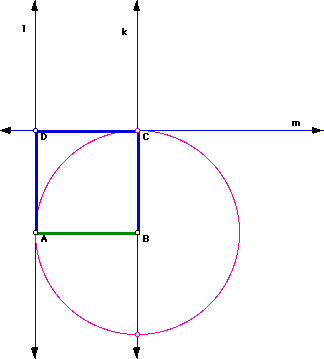
Since lines l and k are both perpendicular to segment AB, then line l is parallel to line k. In a similar fashion, since lines l and k are both perpendicular to line m, then line l is parallel to line k. Segments AB and BC are radii of the same circle. Thus, segment AB is congruent to segment BC. Since line l is parallel to line k and segment AB is congruent to BC, we can say that segment AD is congruent to BC. We also know that all of the angles are right angles at the vertices. This then shows that line m is parallel to segment AB. Hence, segment AB is congruent to segment CD. By definition of a square, ABCD is a square.
Part C
Given two points, construct a regular hexagon with the two points as adjacent vertices.
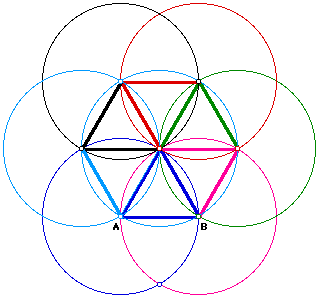
Click here for a GSP Script that will construct a regular hexagon, given two points, with those two points as adjacent vertices.
Why does this construction work?
This construction begins by constructing an equilateral triangle, having one of its sides containing the two original points, A and B, that also serve as adjacent vertices. Then we continue constructing five more equilateral triangles built around the original equilateral triangle. Since we are using a side from the original equilateral triangle to construct our new equilateral triangle, we are assured that each side is congruent to the original side that was given, segment AB. We repeat the process over five times and finally have a six sided figure, composed of six equilateral triangles. This six sided figure is a regular hexagon.
| Problem 3 |
Given a line segment and an integer n = 2, 3, 4, ..., construct points on the segment which divide it into n segments of equal length. Do the GSP Sketch and Script for the case n = 5, and explain why your method works in the general case.
After constructing points on the line segment which divide it into 2, 3, and 4 segments, a general rule for constructing the points lies in knowing that if you want to divide the segment into n equal segments, you will need n-1 segments (blue in picture) that divide the segment into n segments.
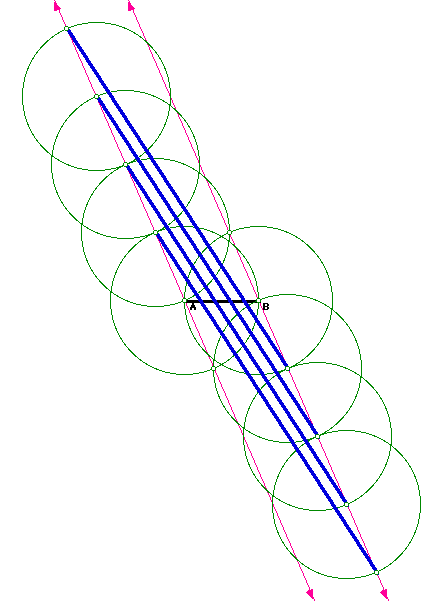
Click here for a GSP Script for the case n=5.
Why does this construction work?
The construction method works based on properties about congruent triangles, similar triangles, and parallel lines.
Return to Foundations of Geometry I Homepage