



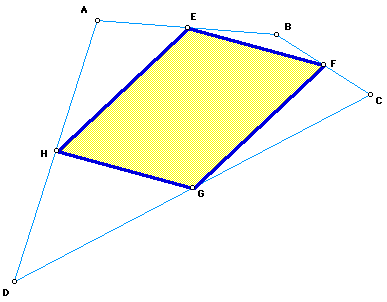
Observation:
Notice the parallelogram becomes a straight line (parallelogram is degenerate)
when one pair of opposite sides of the quadrangle become parallel (dotted
blue lines indicate parallel lines).

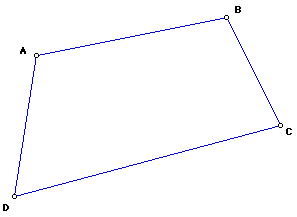
Next we would like to prove the relation: when the midpoints of the sides
of a quadrangle, labeled as E, F, G, and H, are joined in order, a parallelogram
is formed, namely EFGH.
First we construct quadrangle ABCD. Then construct the midpoints of the
sides of the quadrangle, labeled as E, F, G, and H, in order.
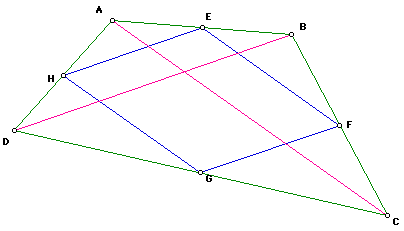
Since E is the midpoint of AB and F is the midpoint of BC, AE=EB and BF=FC. By the theorem that states, in a triangle, if a line bisects two sides of the triangle, it is parallel to the third side, we can conclude that EF || AC. Similarly, since H is the midpoint of AD and G is the midpoint DC, we know AH=HD and CG=DG. By the same theorem previously mentioned, HG || AC. Using the transitive property, EF || HG. Now we repeat this process over again to show that EH || FG. Consequently, we have shown that EF || HG and EH || FG. Therefore, by the definition of a parallelogram, we have shown that EFGH is a parallelogram.
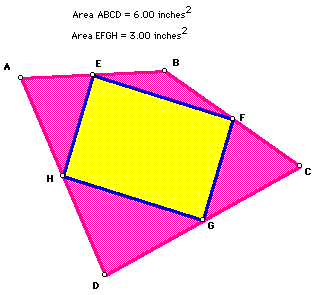
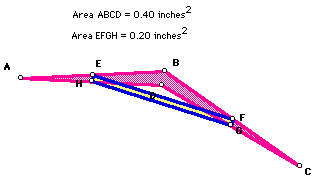
Now it seems natural to prove the relationship between the areas; that
is, the area of the quadrangle ABCD is twice that of the area of
the parallelogram EFGH or equivalently, the area of the parallelogram EFGH
is one half that of the area of the quadrangle ABCD.
We begin by constructing a quadrangle ABCD with midpoint of each side connected
in order, EFGH. Construct the diagonals of the quadrangle ABCD, AC and BD.
Lastly, construct the diagonal of parallelogram FXYZ, FY. We know that FXYZ
is a parallelogram based on the previous proof showing EFGH was a parallelogram.
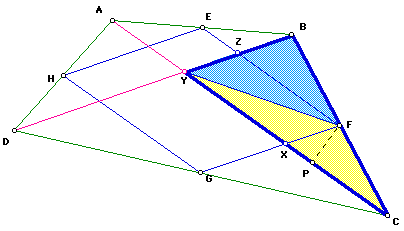
Based on a previous theorem (page 12, #14) we already proved, we have
YX=XC. YX is the base of triangle FXY and XC is the base of the triangle
FCX. FP is also the height for the two triangles FXY and FCX. Consequently,
the area for those two triangles will be equal, since the area formula for
a triangle is 1/2 bh, and both triangles share the same base and same height.
If we parallel the same steps for triangles FZY and FZB, we can show that
their areas are equal. If we think of the area of triangle FCX and triangle
FXY both equal to x and similarly, the area of triangle FZY and triangle
FZB both equal to y, then the total area of triangle BCY = 2x +2y. Simplifying
this algebraically, we have area of triangle BCY= 2(x+y). Consequently,
the area of triangle BCY is twice that of the parallelogram FXYZ, since
the area of parallelogram FXYZ = x+ y. If we repeat this process over three
more times for each section of the quadrangle; that is, triangle DYC, BYA,
and DYA, then it follows naturally that the total area of the quadrangle
ABCD will be twice that of the parallelogram EFGH.
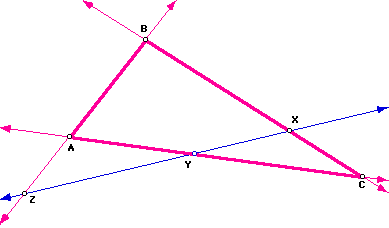
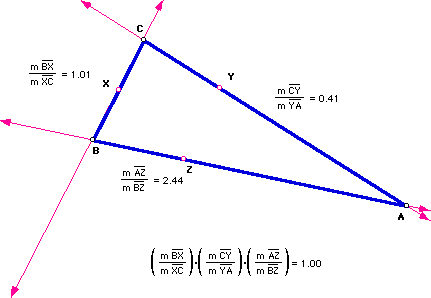
We want to investigate the following two questions:
1. What is the relation between the ratios BX/CX, CY/AY, and AZ/BZ?
2. If the relation holds, must X, Y, and Z be collinear?
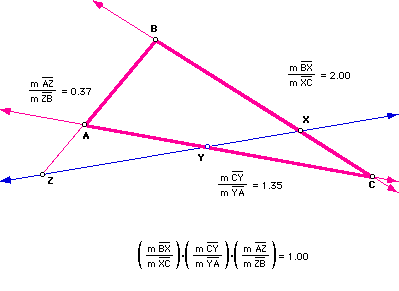
Clearly, when you multiply the ratios together, the relationship between
the ratios is 1.
For a demonstration that shows this relation holds when X, Y, and Z are
collinear, click here.
We can prove this relationship. Begin with the following picture where we
constructed a parallel line, AD, to line CB. Using this parallel line and
similar triangles, we will prove that the relationship holds.
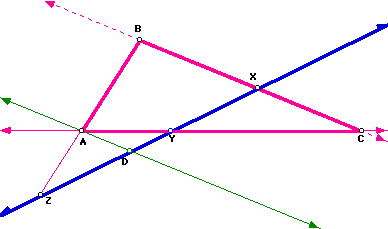
First, we want to show that triangle CXY is similar to ADY. Since AD||BC,
angle A is congruent to angle C and angle ADY is congruent to CXY, because
these angles are alternate interior angles, we know alternating interior
angles are congruent.. Angle AYD is congruent to CYX, since both angles
are vertical and vertical angles are congruent. Therefore, we have shown
that triangle CXY is similar to ADY .
So we have CY/AY=CX/AD.
Second, we want to show that triangle ZAD is similar to triangle ZBX. Since
AD||BC, angle ZAD is congruent to angle ZBX and angle ZDA is congruent to
angle ZXB, because these angles are corresponding angles and corresponding
angles are congruent. We also know that angle AZD is congruent to angle
BZX, since these angles are common to each other. Therefore, we have that
triangle ZAD is similar to triangle ZBX.
So we have XB/BZ=DA/AZ. We also know that ZA/ZB=AD/BX=ZD/ZX.
CY/AY=CX/AD is equivalent to CY/AY * AD/CX = 1.
XB/BZ=DA/AZ is equivalent to BX/BZ * AZ/AD = 1.
Then we have CY/AY * AD/CX * BX/BZ * AZ/AD = CY/AY * BX/CX *AZ/BZ = 1.
Hence, we have shown that the relationship between the ratios is always
1.
Therefore, if X, Y, and Z are collinear, then the relation between the ratios
is 1. Now, let's look at the converse of this statement.
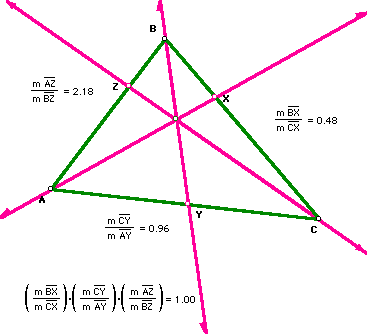
For a demonstration that shows this relation holds when X, Y, and Z are
not collinear , click here.
We want to show that if this relation holds,
then X,Y, and Z are three noncollinear points.
This proof is a proof of a counterexample for the following:
If X, Y, and Z are collinear, then the ratio is 1.
A similar argument, using parallel lines and similar triangles, is used
to prove that this relation holds even if points X, Y, and Z are not collinear.
Begin the proof by constructing two lines, BD and CE, both parallel to line
AX.
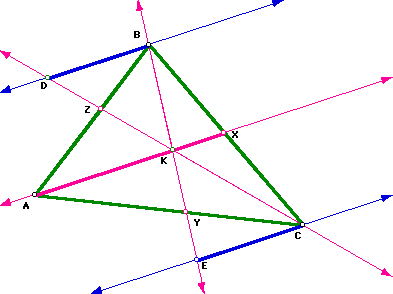
We will show the following triangles similar to one another:
Triangle DBZ similar to Triangle KAZ:
First, we want to show that triangle DBZ is similar to KAZ. Since DB||AK,
angle DBZ is congruent to angle KAZ and angle BDZ is congruent to AKZ, because
these angles are alternate interior angles and we know alternating interior
angles are congruent. Angle BZD is congruent to angle AZK , since both angles
are vertical and vertical angles are congruent. Therefore, we have shown
that triangle DBZ is similar to KAZ . Since corresponding sides of similar
triangles are proportional, this implies that we have
Triangle ECY similar to Triangle KAY:
We can show that these two triangles are similar using the same exact argument
as above, (I will spare you the details) and conclude that
Triangle DBC similar to Triangle KXC:
Next, we want to show that triangle DBC is similar to triangle KXC. Since
DB||KX, angle DBC is congruent to angle KXC and angle BDC is congruent to
angleXKC, because these angles are corresponding angles and corresponding
angles are congruent. We also know that angle BCD is congruent to angle
XKC, since these angles are common to each other. Therefore, we have that
triangle DBC is similar to triangle KXC. Since corresponding sides of similar
triangles are proportional, this implies that we have
Triangle BEC similar to Triangle BKX:
We can also show that these two triangles are similar using the same exact
argument as above, (I will spare you the details) and conclude that
To summarize we have shown the following proportions hold,
This implies the following,
AZ/BZ * CY/AY * BC/CX * BX/BC = AK/BD * EC/AK * BD/KX * KX/EC
and this is equivalent to