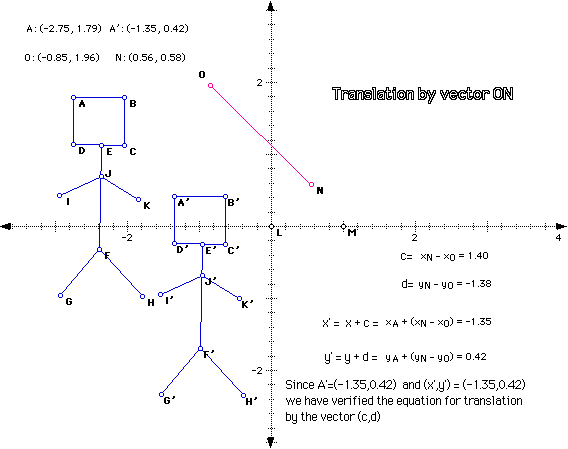
Exploration Using GSP:
Coordinate Characterization of Linear Transformations
GSP problems involving equations for isometries. For each problem
you should turn in a GSP
printout showing the result of your experiment, and a written
explanation of what you did. (The
written explanation may be included as a GSP caption.)
PROBLEM 1
Using the GSP "Measure" menu
and "Calculuate" submenu, verify the
equations for
(a) a translation,
(b) a rotation with center (0,0) and angle theta, and
(c) a reflection with mirror the line through (0,0) at angle theta
with the x-axis.
Part A
We want to verify the following equation for a translation:
Translation by the vector (c,d):
x' = x + c
y' = y + d
Using GSP, Measure Coordinates, we measure the coordinates of point A=(x,y)=(-2.75, 1.79) and A"=(x',y')=(-1.35,0.42) along with the coordinates of the translation vector (c,d) = (1.40,-1.38). We obtain (c,d) by translating point O to the origin. In other words, by finding the change in x we find c, and by finding the change in y we find d. Next, we now know x and c, y and d, and can verify the given equation for a translation as shown below.
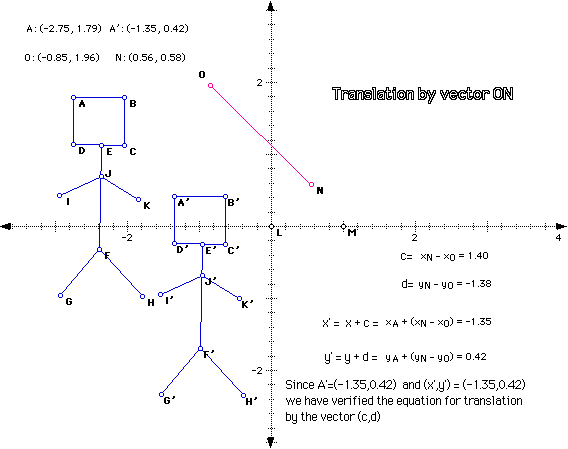
Part B
We want to verify the following equation:
Rotation with center (0,0) and angle theta:
x' = ax - by
y' = bx + ay
a = cos(theta), b = sin(theta)
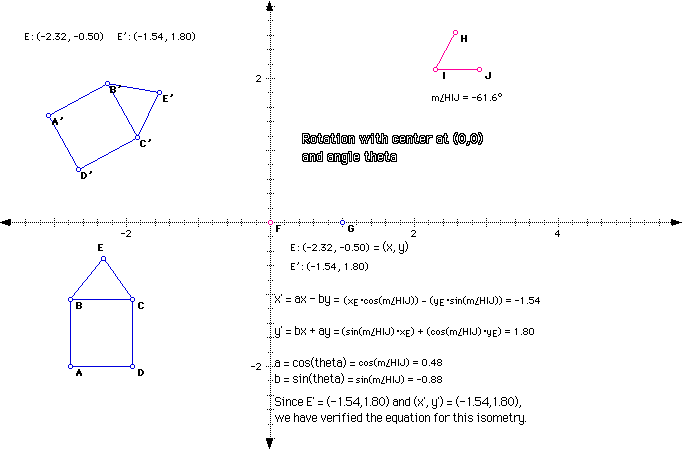
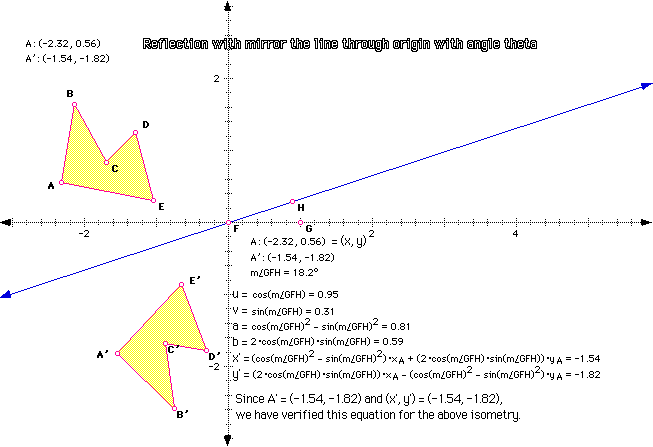
Part C
We want to verify the following equation:
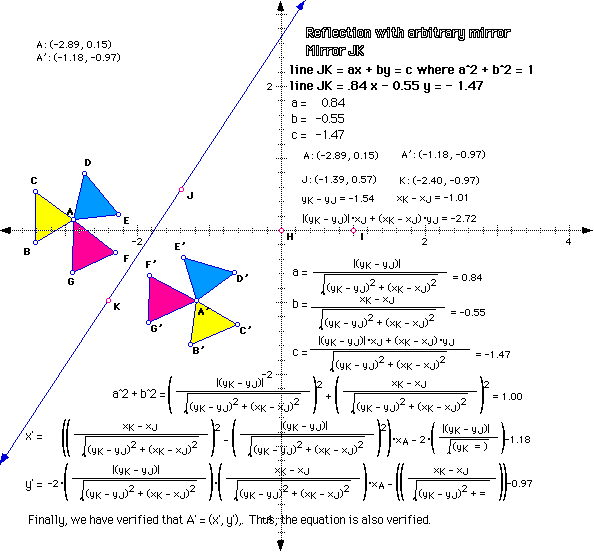
Reflection with mirror the line through (0,0) with angle theta:
x' = ax + by
y' = bx - ay
u = cos(theta), v = sin(theta)
a = u^2 - v^2, b = 2uv
PROBLEM 2
Using the same method, verify the equations
for
(a) a rotation with arbitrary center and angle theta, and
(b) a reflection with arbitrary mirror.
(These equations are given in the book on pages 353-354. You can
get them by combining the
equations of problem 1(b)(c) with translations.)
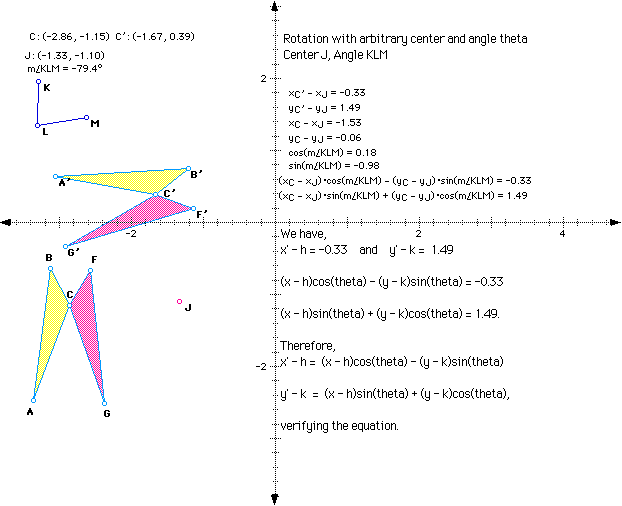
PART A
We want to verify the equation of the Coordinate Form of Rotation about Center(h,k):
(x' - h) = (x - h) cos (theta) - (y - k) sin (theta)
(y' - k) = (x - h) sin (theta) + (y - k) cos (theta)
where theta = measure of angle of rotation
PART B
We want to verify the equation for Coordinate Form of Reflection in a Line
x' = (b^2 - a^2) x - 2aby + 2ac
y' = -2abx - (b^2 - a^2) y + 2bc