y = 3 sin(t)
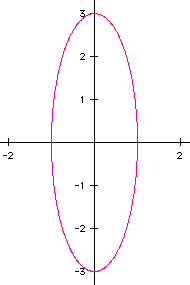

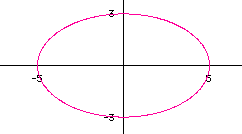
The graph is an ELLIPSE crossing the x axis at -1 and 1 and the
y axis at -3 and 3.
What might you expect when a = -4 and b = -2?
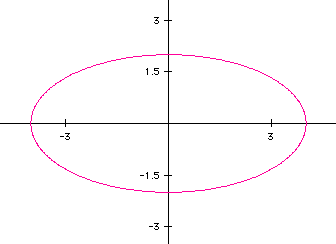
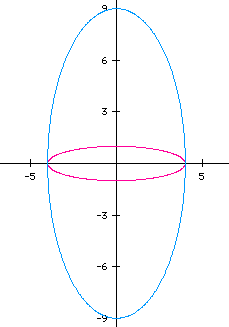
As expected, the ellipse intercepts the x axis at -4 and 4 and the yaxis
at -2 and 2. Notice, however, the ellipse has the x axis as it's major axis
whereas in the previous example the major axis was the y axis. Recall from
your study of the conic sections , particularly the ellipse,
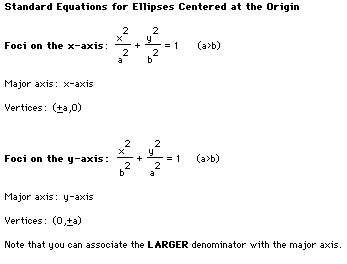
that you can associate ![]() with the major axis. This translates
into our knowledge of parametric equations.
with the major axis. This translates
into our knowledge of parametric equations.
For example, we have our beginning equations
If we divide each side of the equations by a and b respectively, we obtain
the following:
 .
.Now if we square both sides of each equation and add each side of the
equations,

we obtain the following:
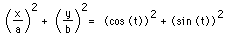 .
.This equation can be simplified further using the trigonometric identity,
![]() .
.
Thus the equation becomes
which is the equation for an ellipse.
Recall from above that when a<b, we get two different cases where the
major axis can be the x-axis or y-axis. What case produces the x-axis as
its major axis? and y-axis as its major axis?
Let's try several more examples to see if there is a pattern. Remember a<b.
Consider the two cases:
a=-4 and b=1 (pink)
a=-4 and b=9 (torquoise). The graph suggest the following ellipses:
In both cases, a<b. The key to identifying the major axis of the ellipse
is looking at the absolute value of a and b. Notiçe when |a|>|b|,
the x-axis is the major axis. When |a|<|b| the y-axis is the major axis.
Now, consider the graph when a=-3 and b=3.

As expected, the ellipse crosses the x-axis at -3 and 3 and the y-axis
at - 3 and 3. Yet, in this case we get a circle which can also be considered
a "special case" of an ellipse.
Notice ![]() .
.
If we consider our equations for an ellipse, since ![]() , our ellipse
will be a circle.
, our ellipse
will be a circle.
Furthermore, when |a|=|b|, the equation will be an ellipse.
What if we consider the case where either a or b is equal to zero?
Let a=p;2 and b=0 , equations are
where ![]() .
.
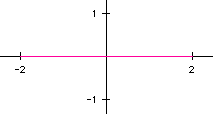
The graph is a straight line whose endpoints are -2 and 2. For every
t, the output is an ordered pair (x,y) which in this case is (-2 cos(t),0).
Thus, a line segment is expected.
Another perspective to answer the question, "What happens if either
a or b is equal to zero?" is to investigate the parametric equations
and their respective graphs as b tends to zero and a is any number.
Letting a=-2 and b tend to zero, consider the following graph where
b=1/2 (pink)
b=1/4 (turquoise)
b=1/8 (green)
b=1/16 (red)
b=1/32 (royal blue)

Notice, as b tends to zero, the ellipse becomes thinner and thinner.
If you let b=0, the ellipse will become a segment.
and the graph
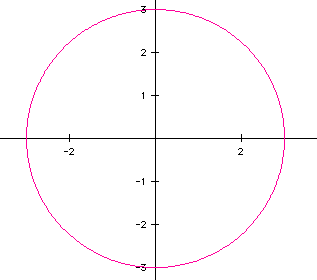
is a CIRCLE whose radius is a=b, in this case a=b=3. You can
also consider this circle as a "special case" of an ellipse where
the x- and y-intercepts are the same. Hence, the distance from the origin
to each vertice is equal and a circle is formed.
Consider when a=b=-6.

As predicted, the graph is a circle whose radius is |-6 | = 6. Remember,
the length of a radius is always positive. Thus, in the parametriç
equations
when a=b, the graph will always be a circle with radius=|a|=|b|.
and the graph is as follows:
The graph is an ellipse with x-intercepts at ![]() and y-intercepts
at
and y-intercepts
at ![]() with |a|>|b|. Using our previous conclusion the graph should have
the x-axis as its major axis. This is a true statement.
with |a|>|b|. Using our previous conclusion the graph should have
the x-axis as its major axis. This is a true statement.
Consider the case when a=4 and b=-2. The associated equations are
and the graph is as follows:
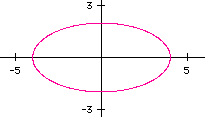
Consider the case when both a and b are both negative and a > b.
Let a=-4 and b=-8. So,
and the graph (pink) is
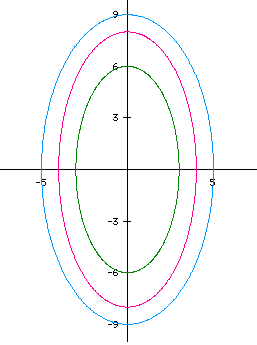
Also, consider several other cases where a=-5 and b=-9 (turquoise) and
a=-3 and b=-6 (green).
Notice the y-axis is the major axis. Recall from our previous discussion,
when |a| < |b|, the major axis is the y-axis.
will always produce an ellipse was shown algebraically. The process involved
squaring both sides of each equation, adding the equations together, and
using a common trigonometric identity. This proved essential in making the
connection. We also explored different cases involving a<b, a=b, and
a>b. Several conclusions drawn were when
a) |a| > |b|, the major axis lies on the x-axis
b) |a| < |b|, the major axis lies on the y-axis
c) a=b, the ellipse will be a circle.
This exploration would prove most beneficial to a secondary mathematics
course when studying ellipses. Why? Parametric equations are not dealt with
heavily in the traditional curriculum. This investigation could be used
after ellipses have been discussed and in conjunction with an introduction
into the concept of parametric equations. Hence, students can sample a taste
of an entirely new concept, parametric equations, along with a connection
to an old concept, ellipses. This mathematical activity allows students
a new perspective on ellipses providing them with a different way to see
ellipses. As a mathematics educator, one of my goals is to provide students
with alternative ways of viewing a mathematical concept. Furthermore, another
goal is to provide opportunities for students to make connections between
mathematics concepts themselves. This exploration fulfills both goals. In
addition, the use of technology is utilized. The technology used provides
students with new mathematical learning experiences while at the same time
the learning is enhanced using technology.