Exploration
of
What does d do?

To begin our investigation of the role that d plays in the quadratic, , it will be necessary to let d assume different values and then graph on the same axes to obtain a picture of what is occuring graphically.

The equations that will be graphed are as follows:
(Equations are graphed in order from right to left)



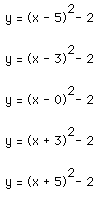
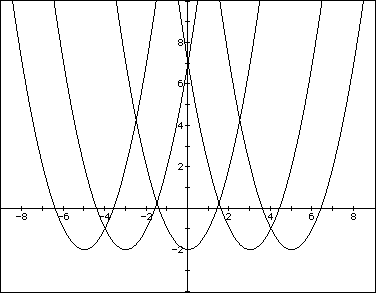
Varying d in the equation causes the graph to shift in position horizontally.

First, when d=0, notice the vertex of the graph is at (0,-2). Since d=0, it follows that the x-coordinate is also equal to 0.

Next, try positive values for d.
When d=5, the graph shifts five places to the right of the original graph when d=0. So the vertex of
the parabola is (5,-2).

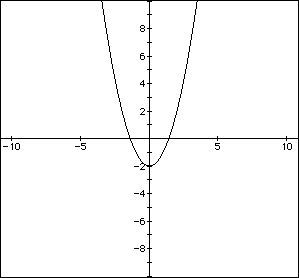
When d=3, we would assume then that the graph would move three places to the right from the original graph where d=0. This is verified by the graph of where d=3. So the vertex

is at (3,-2).


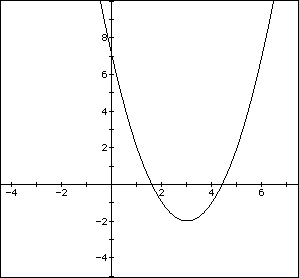
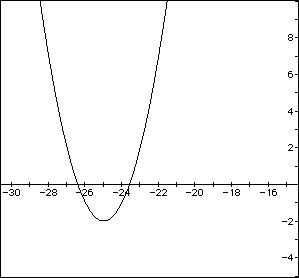
If we want the graph to shift 8 places to the right, all we have to do is alter d by letting d=8. So the equation becomes , where the vertex should be at (8,-2).

Now try negative values for d.
When we substitute negative values in for d, the graph shifts position horizontally to the left. For

instance, when d=-3, the graph moved over three places to the left.

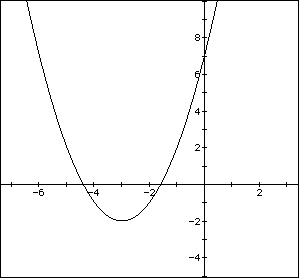
It is important to note here that it appears that d is equal to a positive three in the equation . Nevertheless, the value of d is actually -3. Notice when we substitute d = -3 into the original equation . Simplifying leads to the resulting equation: .

This is important to note to students who often see the positive sign in front of d and assume d is positive. Thus, students haphazardly translate the graph to the right when it should be shifted to the left. It also works the opposite way. When students see the minus sign sitting in front of d, they often assume d is negative and shift the graph's position.
A helpful technique that may prevent students from making this mistake is to place d in parenthesis. For example, shows how d can be placed

in parenthesis to keep it separate from the minus sign in the equation. Thus students do not confuse

the minus sign as being a negative sign and hence shift the graphs incorrectly.
So if you wanted to shift the graph 25 places to the left, d must ascertain the value of -25 in the equation . Thus the new equation where the vertex will be at (-25, -2) is
.

Using this graphing technology allows students opportunities to see the effects that changing one variable, namely d, has on the graph. It is one thing to tell students that changing d translates the graph horizontally. It is however another to let students see for themselves and discover on their own that d causes horizontal shifting of the graph. When students are allowed to make generalizations and draw conclusions on thier own, they experience a sense of involvement and value their learning much more as compared to being told what d does.


Return