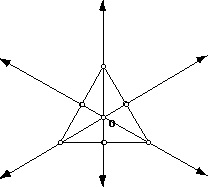
THE ORTHOCENTER OF A TRIANGLE

The ORTHOCENTER (O) of a triangle is the common intersection of the three sides containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.

Our exploration begins with the construction of the orthocenter of a triangle using Geometer Sketchpad.

Construct any triangle along with its altitudes and the intersection of those altitudes is called the orthocenter, O.

In the scalene triangle above, the orthocenter is inside of the triangle where the altitudes meet.

Is this the case for all triangles?

To explore the location of the orthocenter for various shapes of triangles, click here.

Did the location of the orthocenter move?
Intuitively, the answer to this question should be yes. The orthocenter is the intersection of the altitudes. Hence,when you construct new triangles of different shapes and sizes, the location of the orthocenter will also move and change position.

Now that you have explored various shapes of triangles and its effect on the location of the orthocenter, consider several of the distinct cases.

Consider what happens with the position of the orthocenter when the triangle is right, obtuse, and equilateral.

First, intuitively what do you think will happen to the location of the orthocenter when you have one of these triangles?

Now consider each case to see if your assumptions are correct.

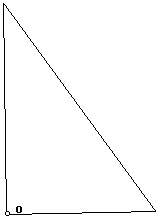
LOCATION OF ORTHOCENTER IN A RIGHT TRIANGLE

When the triangle is right, the orthocenter is the vertex of the triangle at the right angle. Intuitively this makes sense because the orthocenter is where the altitudes intersect. Hence, in a right triangle, the vertex of the right angle is where you would expect the altitudes to meet, at 90 degrees, where the legs of the right triangle are perpendicular.

LOCATION OF ORTHOCENTER IN AN OBTUSE TRIANGLE

When an obtuse triangle is constructed and the altitudes are drawn, the intersection of the altitudes is outside of the triangle. Therefore, the orthocenter moves completely out of the triangle where the altitudes meet. Students often have difficulty with obtuse triangles and their respective altitudes and location of the altitudes. It is important to give students many opportunities dealing with obtuse triangles not just acute triangles.

LOCATION OF ORTHOCENTER IN AN EQUILATERAL TRIANGLE

In an equilateral triangle, the lengths of the segments of the sides of the triangle are all equal. Thus, the distance from the orthocenter to each side of the triangle are equal. In addition, the orthocenter lies on the perpendicular bisector of each side of the triangle. Another conclusion is the distance from the orthocenter to each vertex of the triangle are equal.

Consider another area of exploration dealing with the orthocenter and its relationship to the construction of a parabola.

Recall from your previous exploration: What happened to the position of the orthocenter with triangles of different shapes? Click here for another look.

Notice as the triangles change so does the positon of the orthocenter.

Now consider what happens if you construct a perpendicular to an altitude at the vertex. If this point of intersection is moved along the perperdicular line, trace the orthocenter. What kind of figure is constructed?

Click here for a demonstration.

As the orthocenter is traced, a parabola is constructed.

This exploration and investigation uncovers the connection between the construction of a parabola with the orthocenter of a triangle. Using the orthocenter to construct a parabola gives students a new opportunity to see the connection between these two geometric concepts. It would be rather difficult using paper and pencil methods to investigate this activity and connection. Using GSP, however, provides students with an extraordinary amount of different paths that they take in regards to making conjectures and exploring the connections and commonalities that many of these geometric concepts share and provide. This activity also allows students to see the interplay between the orthocenter and a parabola, two mathematical concepts that seem to have nothing in common without further investigation that is afforded using Geometer Sketchpad.

Return