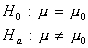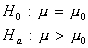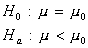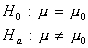www.john-weber.com
Chapter 6: Introduction to Inference
Section 6.2: Tests of Significance
Tests of significance are used to asses the evidence provided by the data about some claim about
a population.
A good start is to read Example 6.7 on page 319 of your text.
Ultimately, if proof of an outcome is very small, then we consider this good evidence that a claim is NOT true.
The reasoning of tests of significance
Tests of significance are based on the idea of the law of large numbers.
The vocabulary of significance tests
- Null Hypothesis (H0): the statement being tested by assessing the evidence against this
statement. The null hypothesis is usually stated in the form of "no effect" or "no difference".
- Alternate Hypothesis (Ha or H1): the claim about a population
for which we are trying to find evidence.
- P–value: Assuming H0 is true, then the p-value is the probability that the
observedoutcome takes a value at least as extreme as the observed outcome. Smaller p-values (i.e., the observed
result is unlikely to occur just by chance), the stronger the evidence against H0.
More detail: Stating hypotheses
- one-tailed tests:
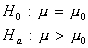
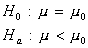
- two-tailed test:
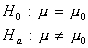
H0 and Ha always refer to the population and NOT to a particular outcome. It
is often easier (and more appropriate) to state H0 and Ha before looking
at the data.
More detail: P–values and statistical significance
The significance level, α: the maximum probability that the data gives evidence AGAINST H0
when H0 is true. α MUST be chosen before the study is undertaken.
A study is statistically significant if it is not likely to happen by chance.
It is easiest to determine statistical significance from the P-value:
- one-tailed test: statistically significant if p-value ≤ α
- two-tailed test: statistically significant if p-value ≤ α/2
The p-value is the smallest level α at which the data are significant.
Tests for a population mean
The steps of hypothesis testing are:
- Identify the parameter (in this case, μ)
- State the hypotheses
- Choose a test statistic (in this case, z-statistic)
- Find the P-value
- State the conclusion
Back to John Weber's MATH 1431 Page
Back to john-weber.com