| Steps |
Key Sequence |
Screens |
** To find P(X = k) use binompdf. The function has three (3) arguments:
number of trials (n), probability of a success (p), number of successes (k).
In other words, binompdf(n, p, k). ** |
| Find the binomial probability function |
Press 2nd then VARS |
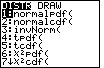 |
| |
Press 0 (for binompdf) |
 |
| Example 1: Let n = 12, p = 0.3 and k = 4 |
binompdf(12, 0.3, 4) |
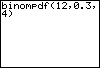 |
| |
ENTER |
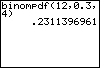 |
| |
** To find P(X ≤ k) use binomcdf. The function has three (3) arguments:
number of trials (n), probability of a success (p), number of successes (k).
In other words, binomcdf(n, p, k).** |
| Find the binomial cumulative function |
Press 2nd then VARS |
 |
| |
Press ALPHA, then MATH (for binomcdf) |
 |
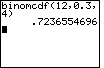
Example 2: Let n = 12, p = 0.3 and k = 4
This finds P(X ≤ 4)
NOTE: P(X ≤ 4) = P(X = 4) + P(X = 3)
+ P(X = 2) + P(X = 1) + P(X = 0) |
binomcdf(12,0.3,4) |
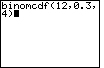 |
| |
ENTER |
 |
** To find P(X ≥ k) use binomcdf. The function has three (3) arguments:
number of trials (n), probability of a success (p), number of successes (k).
NOTE: P(X > k) = 1 – binomcdf(n, p, k) and
P(X ≥ k) = 1 – binomcdf(n, p, k–1).** |
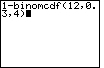
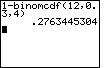
Example 3: Let n = 12, p = 0.3 and k = 4
To find P(X > 4)
use 1 – binomcdf(12,0.3,4) |
1 – binomcdf(12,0.3,4) |
 |
| |
ENTER |
 |









