HOW TO FIND THE SCORE FOR A GIVEN AREA UNDER THE NORMAL CURVE ON THE TI83

Steps	Key Sequence	Screens
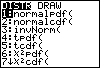
1. Find the inverse normal curve function	Press 2nd then VARS
	Press 3 (for invNorm)
** This function has three (3) arguments. They are: area, mean, standard deviation. **
** Area MUST be between 0 and 1.
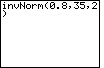
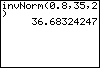
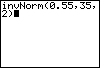
Example 1: Let mean = 35 and standard deviation = 2
Case 1: Find the number x such that the proportion of observations that are less than x in a normal distribution is 0.8. In other words, the area to the left of x is 0.8.	invNorm(0.8,35,2)
	ENTER
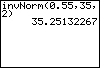
Case 2: Find the number x such that 45% of all observations from a normal distribution are greater than x. In other words, the area to the right of x is 0.45 and the area to the left is 0.55.	invNorm(0.55,35,2)
	ENTER
Example 2: Standard Normal Curve where mean = 0 and standard deviation = 1
** The standard normal curve uses z, where z = (x – mean)/(standard deviation).
** Rearranging for x: x = mean + z * standard deviation.
** For the standard normal curve, the invNorm function will use ONLY one (1) argument, area. By default mean = 0 and standard deviation = 1.
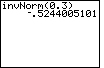
Case 1: Find the number z such that the area under a normal distribution is 0.3 to the left of z.	invNorm(0.3)
	ENTER
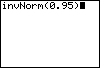
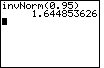
Case 2: Find the number z such that 5% of all observations from a normal distribution are greater than z. In other words, the area to the right of x is 0.05 and the area to the left is 0.95.	invNorm(0.95)
	ENTER