
64.5,2.5)
64.5,2.5)
64.5,2.5)
| Steps | Key Sequence | Screens |
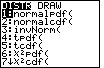
| 1. Find the normal curve function | Press 2nd then VARS |  |
| Press 2 (for normalcdf) |  |
|
| ** This function has four (4) arguments. They are: lower bound, upper bound, mean, standard deviation. ** | ||
| Example 1: Let mean = 64.5 and standard deviation = 2.5 | ||
| ** To type in E use 2nd then comma. To type in a negative sign, use (-) button. | ||
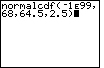
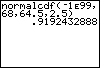
| Case 1: Find the area to the left of x = 68 on the normal curve. | normalcdf(-1E99,68, 64.5,2.5) |
 |
| ENTER |  |
|
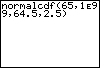
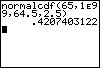
| Case 2: Find the area to the right of x = 65 on the normal curve. | normalcdf(65,1E99, 64.5,2.5) |
 |
| ENTER |  |
|
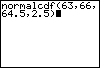
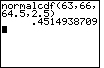
| Case 3: Find the area between x = 63 and x = 66 on the normal curve. | normalcdf(63,66, 64.5,2.5) |
 |
| ENTER |  |
|
| Example 2: Standard Normal Curve where mean = 0 and standard deviation = 1 | ||
| ** The standard normal curve uses z, where z = (x – mean)/(standard deviation). | ||
| ** The normalcdf function will use ONLY two (2) arguments. They are: lower bound and upper bound. By default mean = 0 and standard deviation = 1. | ||
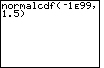
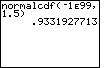
| Case 1: Find the area to the left of z = 1.5 on the normal curve. | normalcdf(-1E99,1.5) |  |
| ENTER |  |
|
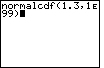
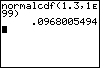
| Case 2: Find the area to the right of z = 1.3 on the normal curve. | normalcdf(1.3,1E99) |  |
| ENTER |  |
|
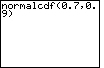
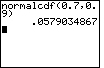
| Case 3: Find the area between z = 0.7 and z = 0.9 on the normal curve. | normalcdf(0.7,0.9) |  |
| ENTER |  |
|