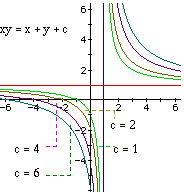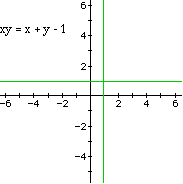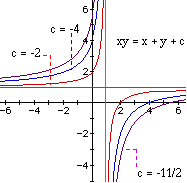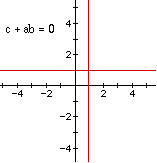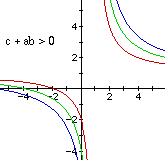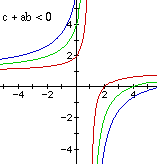NOTE: Enlarge your screen to allow pictures to be two per line! Also,
please be seated...these pictures are outstanding!!
Consider the graphs of the equations
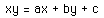
When a = 1, b = 1, c = 1, the graph is a hyperbola with asymptotes at x
= 1, y = 1.
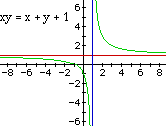
Look at a few graphs with c = 2, 4, 6.
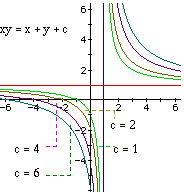
Now, going in the opposite direction, some interesting things start happening.
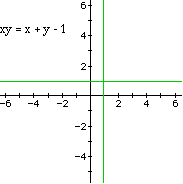
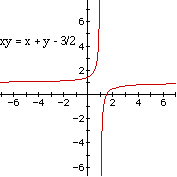
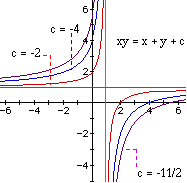
Consider what is happening to the equation algebraically.
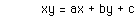
Solve this for y to get a better feel for the function.
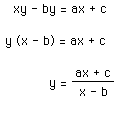
Dividing these to isolate the x:
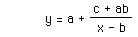
Now, looking at this equation, things become a bit clearer.
When x = b, we have an asymptote because that fraction would be undefined
(and therefore cannot occur for this function).
If c + ab = 0, the equation is y = a which is just a vertical line, no longer
a hyperbola. This is the other asymptote.
When c + ab is positive, you have a family of curves in quadrant I and III.
When c + ab is negative, you have a family of curves in quadrant II and
IV.
Here is a recap with pictures.
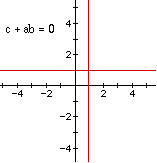
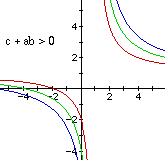
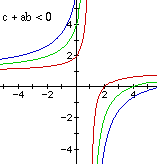
Return to Sherry's class page