

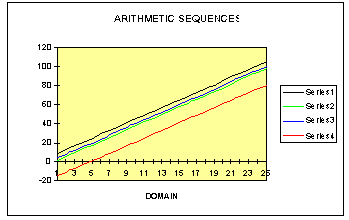
If we look at the graphs of these sequences, we notice that they are
all linear. The black line is the graph of 4n+5. The blue line is the
graph of 4n. The green line is the graph of 4n-2 and the red line is the
graph of 4n-19.
Do all arithmetic sequences have linear graphs? Let's examine another
arithmetic sequence to see if its graph is linear. We are going to examine
the sequence 1/2n and variations of this sequence. Examine the following
spreadsheet.
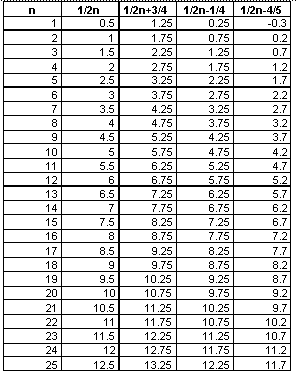
From examining the spreadsheet and from our knowledge of functions and
graphs, these sequences appear to have linear graphs also. Let's graph
them to find out.
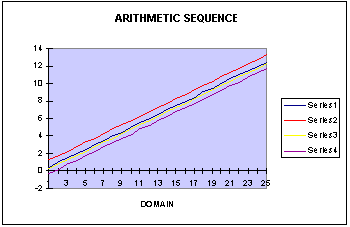
Our hunch was right. These sequences have linear graphs. The red line
is the graph of 1/2n+3/4. The blue line is the graph of 1/2n. The yellow
line is the graph of 1/2n-1/4. The purple line is the graph of 1/2n-4/5.
What can you conclude about arithmetic sequences? Are they all linear?
How are these sequences related to other functions?
Examples of Geometric Sequences
The following geometric sequences are 2^n and variations on this sequence.

Now, graph these sequences to determine their shape.
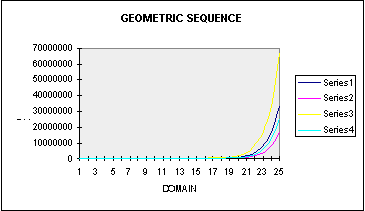
From observing the above graphs, the shape of these geometric sequences
are exponential. Let's do another example. In this example, we are investigating
the sequence of (1/3)^n and variations on it. Look at the following spreadsheet.

Are the graphs of these geometric sequences similar to the graphs of
the above geometric sequences? Let's graph them to see.
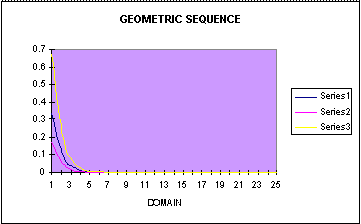
The graphs of these sequences have a similar shape to the previous ones.
But unlike the previous ones, these graphs are decreasing exponentially;
whereas, the previous ones were increasing exponentially. Will all geometric
sequences be exponential? How are these sequences related to other functions?
Hopefully, by studying the graphs of different sequences, students will
obtain a better understanding of sequences and how they are related to other
functions.