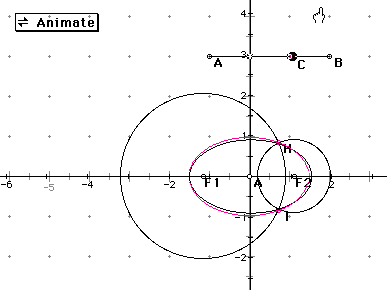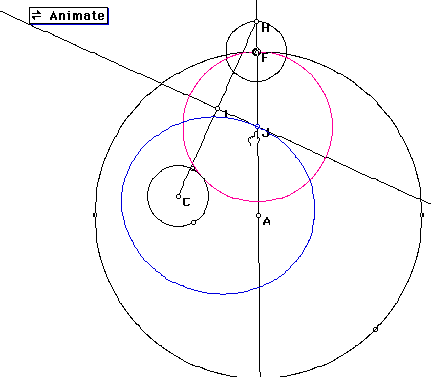
Reponse to "Investigations of Ellipses"

I I constructed a circle with center A, point C inside the circle, and point D on the circle. I constructed segment CD, found its midpoint, and its perpendicular bisector. I traced the locus of the perpendicular bisector as point D traveled around the circle. The results of that construction are below. As you can see, the outlined figure appears to be an ellipse with foci at A and C. I then made a script to repeat this construction for future use.

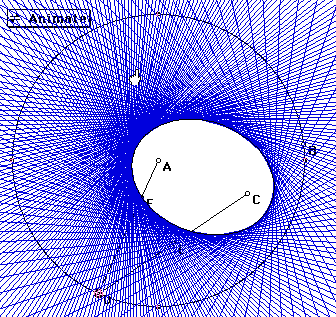
I did this several times moving C around to several positions closer to the center and further away from the center. The closer C got to the center, the more circular the ellipse. The further away C got from the center, the more elongated the ellipse. When C was exactly on the center, the line enclosed a concentric circle. When C was on the circle, the ellipse degenerated to a line.

II I used my script to construct a new circle as before. Sometimes I have to drag my point that is supposed to be inside back into my circle. This time I added a new segment, connecting the center, A, and the point on the circle, D. The intersection of the new segment and the perpendicular bisector of the original segment, F, was then traced as D moved around the circle. It was discovered that F is the point of tangency of the ellipse that was being traced by the perpendicular bisector in the sketch.

The problem now becomes to prove that the figure above is indeed an ellipse.

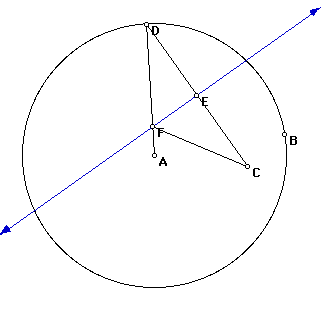
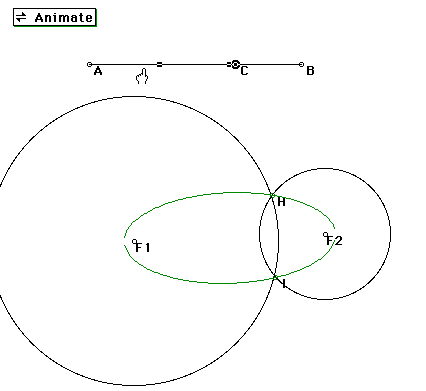
III I constructed the Two-pins-and-a-string ellipse using GSP as instructed in the handout. The following picture shows the results. The actual animation can be experienced if you open the file labeled Two-pins-and-a string.

I conjecture that the figure is an ellipse. To prove this, I connected constructed segment F1H and segment F2H as shown below. Since these are also the lengths of segments AC and CB respectively and AB is a constant length, the the sum of F1H and F2H is a constant length. Thus the figure is an ellipse.

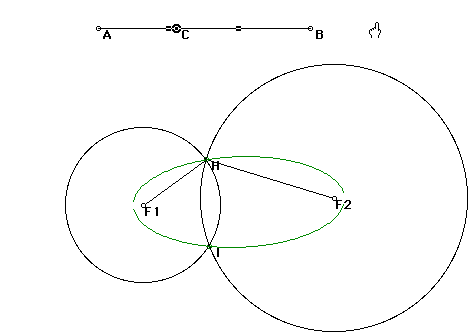
As F1 and F2 get closer, the ellipse becomes more circular and becomes a circle when the two converge as the center. As F1 and F2 get farther apart, the ellipse becomes thinner. The maximum possible distance for F1 and F2 to be apart is the length of segment AB.

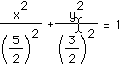
IV I followed the instructions on the handout and conjectured that the equation of the ellipse was:

I copied and pasted the picture into the original GSP document and adjusted the scales. If you look at the picture below you can see that the conjecture seemed correct.

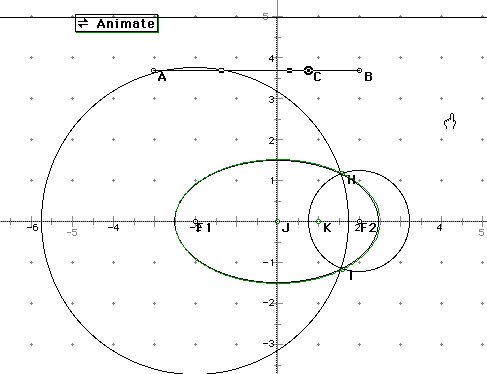
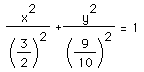
V. I graphed the equation on Algebra Xpressor :

I then pasted the ellipse onto GSP and created the two-pins-and-a string construction as before. I put my centers at (1.2,0) and (-1.2,0). I calculated these focal points using the equation c^2=a^2-b^2. The line segment must be twice the "a" length, because "2a" is the lenght of the major axis. The results are below. I believe the reason that the two do not match exactly is because it is difficult to find 1.2 exactly on the x-axis.

VI I constructed the tangent circles by the directions given in part VI. You can open the file Tangent Circles Ellipse. For this blue figure (see below) to be an ellipse, the distance CJ + the distance AJ must be a constant. The length of CJ is equal to the length of HJ. Therefore CJ+AJ = HJ +AJ and HJ + AJ is a fixed distance. Therefore the sum of the focal radii is a constant and the blue figure is an ellipse.