Circles and the movements of the graph
by Andrew Eager
The definition of a circle is the locus of all points in a plane that are
equidistant from a fixed point. In other words, if you have a point and
you take a line segment ,at any length,and you rotate it in either a clockwise or
counterclockwise direction the beginning and the end will meet to create
a circle.
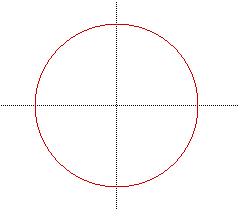
The standard equation for the circle is 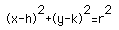 . The constants
h,k effect the location of the center of the circle. Here is an example
of the h,k effecting the location of the center. First,here is a graph that
hasn't move and then the moved graph.
. The constants
h,k effect the location of the center of the circle. Here is an example
of the h,k effecting the location of the center. First,here is a graph that
hasn't move and then the moved graph.
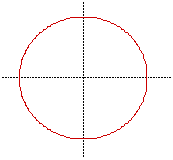

Example 1 equation is x^2+y^2=16 Example 2 equation (x-2)^2+(y-2)^2=16
Notice how the graph in example 2 moved up and to the right away from the
origin. It did that because I put 2 in the equation for the h,k. If I would
have put negatives in the equation it(graph) would have gone to the left
and down. There is also another way the graph can be effected. It is by
changing the value for the r in the equation. The larger the number for
r gets the larger the circle and the same for smaller number means smaller
graph. Here is an example of the graph's size changing from small to large.
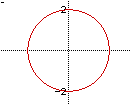
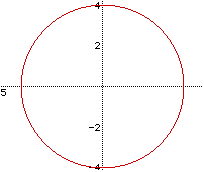
The equation for this graph is 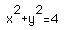 . The equation
for this graph is
. The equation
for this graph is 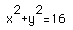
Notice how the size of the graph increases as the radius (r) increases.
To get the length of the radius you would have to take the square root of
r^2 in the standard form.
A circle can also be translated for the location which it is at. To translate
means to move or shift the graph a certain distance. When given a translation
you add the center coorindiates with the numbers in the translation. Example:
T(2,3) and the center is (2,2). Add the first variable to get 4 and the
second to get 5. Now the graph's center is at (4,5). Watch the movement
of the graphs to see the translation.
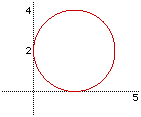
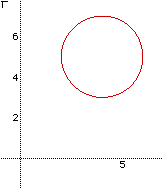
The equation is (x-2)^2+(y-2)^2=4. With the translation the second equation
will be (x-4)^2+(y-5)^2=4 Notice how the graph's center moved from 2,2 to
4,5 after the translation.
Eccentricity
First, here is the equation of eccentricity for any conic, e=c/a. Eccentricity
of a circle is very easy to find. The reason that eccentricity is found
easily in a circle is because there isn't a (c) in an equation of a circle.
Therefore, the eccentricity of a circle is always zero.
The general form for all conics is where the equations for the circle came
from. The equation for the general form is 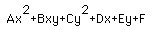 . The equations
for all the conics come from this basic equation.
. The equations
for all the conics come from this basic equation.
Return to Journal Two


![]() . The constants
h,k effect the location of the center of the circle. Here is an example
of the h,k effecting the location of the center. First,here is a graph that
hasn't move and then the moved graph.
. The constants
h,k effect the location of the center of the circle. Here is an example
of the h,k effecting the location of the center. First,here is a graph that
hasn't move and then the moved graph.




