Parametric Curves :An exploration in mathematics and the construction of a web page.


by Mary Wilson Eager

EMT assignment 10 piqued my interest in the mathematics of parametric curves. In that assignment a parametric curve in a plane is defined as "a pair of functions , x=f(t) and y=g(t), where the two continous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t. In many applications, we think of x and y varying with time t."

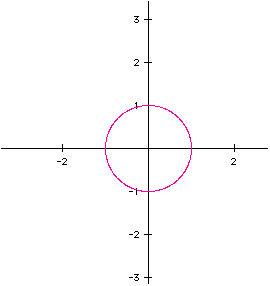
To investigate the problems I chose to use Xfunction as my graphing utility. As a starting point I entered x=cos(t) and y=sin(t) for 0<t<6.28. The following curve results.


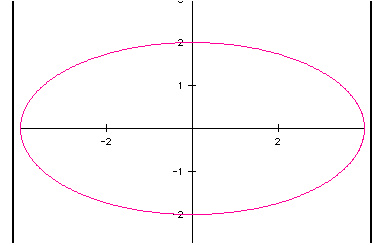
The circle, center at the origin, has a radius of one unit. Knowing the values of cos(t) and sin (t) range from one to negative one, its reasonable the ordered pair (x, y) would do likewise. The pythagorean relationship explains why the curve is a circle. If the equations are modified to include a scalar the radius of the circle changes if the scalar is the same number for both x and y. When the scalars differ for x and y, the curve becomes an ellipse centered at the origin with intercepts of (a,0), (-a,0), (0,b) and (0,-b). This is illustrated for the equations x=4cos(t) and y=2sin(t).




When the following equations, x= cos(at) and y=sin(bt), are entered with various values of a and b interesting curves result. Appropriate these are called "bow tie" curves. The graph below shows x=cos(t) and y=sin(2t) with a range of t from 0 to 6.28.



As the values of a and b change, the number of loops change, the x and y intercepts change as seen for the graph of x=cos(3t) and y=sin(2t).


By using the graphing utility and trying many different values of a and b, some patterns emerge. When a is odd there are two times a places when x=0 and two times b places when y=0. When a is even there are a places where x=0 and b places where y=0. These intercepts are found at (0, sin(b*pi/2a)) and (cos(pi/b), 0). The envelope of curves seems to form a square or a rectangle with length the scalar in front of the cosine function and width the scalar in front of the sine function. I will close this discussion with the graphs of x=cos(5t) and y=sin(3t).



The last step to this exploration will be getting it to come up on my web page...If you're reading it I must have been successful. WOW!