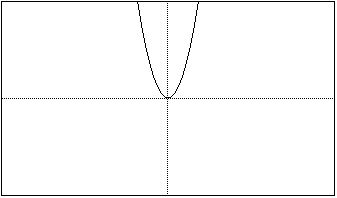
A parabola is defined as the locus of all points in a given plane that
are the same distance from the given point, called the focus, and a given
line, called the directrix.

The above graph is the parent graph which has the equation y=x^2.
The vertex is at the origin (0,0). The graph always intercepts the coordinates
(1,1) and (-1,1).
The standard equation of the parabola is (x-h)^2=4p(y-k). The constant
h represents the x-coordinate of the vertex. Whereas the k
constant represents the y-coordinate of the vertex. The latus rectum of
the graph is represented by 4p .
The parabola can also be represented by two "general form"
equations. These equations are y^2+Dx+Ey+F=0, when the directrix
is parallel to the y-axis, or
x^2+Dx+Ey+F=0, when the directrix is parallel to the x-axis.