From Playfair [3], "A plane rectilineal angle is the inclination of two straight lines to one another, which meet together, but are not in the same straight line.' The mapping is in Figure 9. We can see that the mapping consists of two arcs that meet in a point. Is the angle the same? Let's move on to the next definition, that of the perpendicular, to get some sense of the answer.next
Figure 9
From Playfair, "When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the angles is called a right angle; and the straight line which stands on the other, is called a perpendicular to it." Here we go! next
Figure 10
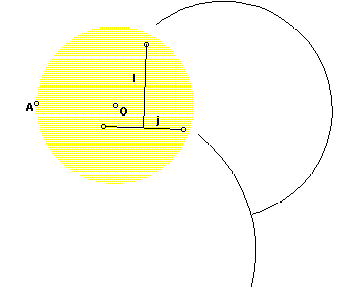
And what about "An obtuse angle is that which is greater than a right angle." and "An acute angle is that which is less than a right angle." [3].next
Figure 11
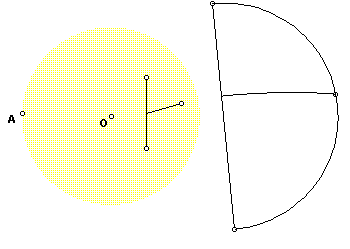
Notice that all of the mappings of the angles are arcs. Since the angle of the arcs one to another differs, in the straight line sense, depending on where you measure, how can we relate the straight line angles inside the circle to the angles between arcs outside the circle? The next series of figures gives us an idea. Here we show the mapping of a vertical line that is joined at the center by another line segment. The vertical line segment maps to a major arc, while the joining line segment maps to a minor arc. next
Figure 12 a
next
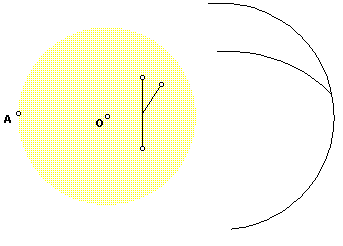
Figure 12 b
next
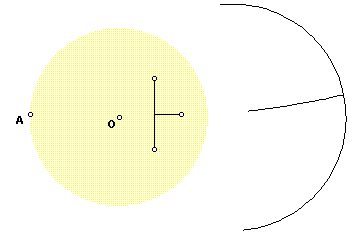
Figure 12c
next
Perhaps there's a relation between the straight angles and the intercepted arcs of the semicircle formed from the major arc and a line parallel to the vertical line in the disk. Figure 13 provides a construction for exploration.next
Figure 13
The mappings we've viewed relative to angles are easily extended to triangles and quadrilaterals, etc. In this exploration we will conclude with a quick look at circles and their maps. Figure 14 is the mapping of a circle from a disk to the plane.next
Figure 14
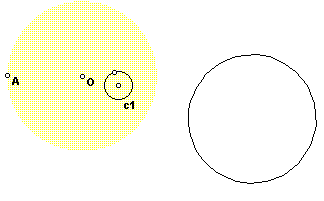
So, a circle is a circle. As a matter of fact, except for the difference in the sizes, this is not very interesting except at the center and around the boundaries. As the circumference of the circle approaches the center of the disk its mapping approaches a straight line in Euclidean space (Figure 15).next
Figure 15
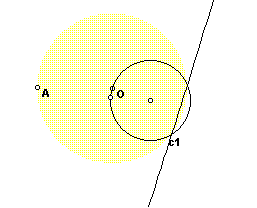
Circles at the boundaries map to exterior intersecting circles. You will recall these are the same lines we looked at earlier. next
Figure 16
These circles are orthogonal circles which leads to another exploration.back to figure The following GSP script for creating orthogonal circles [1] is provided for the reader to verify.next
Figure 17
orthoc.gss
	Given:   Point O,   Point A,   Point B
---------------
Steps:
   1. Let 1 = Circle with center at Point O passing through Point A.
   2. Let [j] = Line between Point O and Point B.
   3. Let [k] = Perpendicular to Line [j] through Point B.
   4. Let E = Intersection of Circle 1 and Line [k].
   5. Let [E] = Intersection of Circle 1 and Line [k].
   6. Let [l] = Line between Point O and Point E.
   7. Let n = Perpendicular to Line [l] through Point E.
   8. Let [F] = Intersection of Line n and Line [j].
   9. Let p = Segment between Point B and Point [F].
   10. Let [G] = Midpoint of Segment p.
   11. Let q = Perpendicular to Segment p through Midpoint [G].
   12. Let [H] = Random point on Line q.
   13. Let 2 = Circle with center at Point [H] passing through Point B.
   14. Let [I] = Intersection of Circle 2 and Line n.

Conclusion

The use of GSP to investigate relationships between Euclidean and alternative geometries provides much insight to these relationships. But, more importantly, the effort can stimulate the desire do do even more exploration. I have only cited the demonstration aspects of my explorations related to Euclidean definitions and Poincare circles. What I have not cited are the many interesting, though unorganized, tangents on which this exploration led me far afield from Poincare's. Though most of these led to no startling conclusions, the exploration itself was worthwhile. To paraphrase a saying oft used, the reward lies as much in the exploration as in the discovery.

first page/ previous page/ top of this page/ home page

  1. Bill Juraschek," Investigating Circles in the Poincare Disk Using Geometer's Sketchpad", The College Mathematics Journal ,Vol 25,Nbr. 2, March 1994,p146
  2. [2] "The Geometer's Sketchpad", Version 3, Key Curriculum Press, Berkeley, CA, 1994.
  3. [3] John Playfair, Elements Geometry - Containing the First Six Books of Euclid, W.E Dean, Printer and Publisher, 2 Ann Street, New York, 1849