
Department of Mathematics Education
EMT 469


First construct perpendicular lines in which to build our triangle upon.
From the intersection point I, strike an arc of length b onto the perpendicular
and call its intersection point K.

Next, construct the midpoint of segment b and call it R.
In geometry, there exists a theorem which states that the three medians
of a triangle intersect at a point in which it divides each of the lengths
of the medians into a ratio of 2:1. Thus, the next step in the construction
is to trisect our original medians m(a) and m(b).
Using 1/3 the length of m(b) as a radius, construct a circle centered at
point R. Then from point K construct a circle with radius the length of
2/3 the length of m(a). Call the circles' point of intersection S. Then
construct rays from K and R through S.
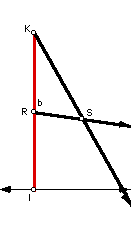
Now from point K copy m(a) onto the ray emanating from point K and call
its intersection with the ray Q. Likewise, from point R copy m(b) onto the
ray emanating from R and call its intersection with the ray T.
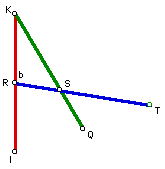
Now construct segments IT and TK.

Thus, the construction is complete.
To see a GSP script click here.
Back to table of contents