
The Department of Mathematics Education
Problem-Solving Using Graphing Calculators
by
June Jones
University of Georgia
Spring 1997
Problem, Questions
This paper will examine difficulties in problem-solving among fifty-six
college freshmen in precalculus algebra.
Questions to consider:
(1) How do the problem-solving difficulties of these students
fit the categories of difficulties as determined by the literature? and
(2) How does use of a graphing calculator affect problem-solving?
Review of Prior Research
According to Butler & Wren (1965), there are four basic types of problem-solving
difficulties: comprehension, structure, operation, and judgement. Researchers
have also studied the ways students learn to problem-solve. The intent
was to formulate a concise procedure for the students to follow so that
the difficulties could be lessened and eventually completely eliminated.
Five basic methods were identified: restatement, analysis, analogies, dependencies,
and graphic. Studies show that none of the methods stands out as best and
that all yield acceptable results. Each method has its own merit and they
can be used in conjunction to best satisfy the needs of any variety of problems
(Butler & Wren, 1965).
Besides the above stated broad-based information, there has been much research
into specific areas within problem-solving. A few of them are related below.
The third NAEP Mathematics Assessment revealed that 13- and 17-year-olds
were improving (from 1973 to 1982) in basic skills, but still lacked a deep
understanding of mathematics and its applications. It also reported that
students had positive attitudes toward mathematics, problem-solving and
computers (Carpenter, Lindquist, Matthews & Silver, 1983).
Rich (1990) confirmed that the graphing calculator in precalculus improved
students' understanding of graphing and provided an appropriate problem-solving
technique.
Carter (1995) found that the graphing calculator seemingly led to improved
problem-solving, as less time was consumed with algebraic manipulations.
He also reported that the students used the calculators as a monitoring
aid while solving word problems. Bitter & Hatfield (1991) also found
that students using calculators showed improved problem-solving skills.
Szetela & Super (1987) found a better attitude toward problem-solving
when the calculator was used. However, the scores were not significantly
higher for those students than their counterparts who did not use a calculator.
Schoenfeld (1988) found in a study with geometry students that they could
feel confident about their skills and still not make the connection within
the topics.
The volume of research has prompted responses from many sources. The National
Council of Teachers of Mathematics devoted its 1980 Yearbook to Problem
Solving in School Mathematics. The National Council of Supervisors of Mathematics
placed great emphasis on problem-solving (Carl, 1989). The NCTM Standards
(1989) also emphasized problem-solving at all levels and encouraged extensive
use of the calculator. The National Research Council compiled Everybody
Counts (1989) and Moving Beyond Myths (1991), which provided a wealth of
statistics on various demographics, many of which affect student problem-solving.
Madison and Hart reported much of the same in A Challenge of Numbers (1990).
The NCTM Position Statement (1996) states:
Research and experience have clearly demonstrated the potential
of calculators to enhance students' learning in mathematics. The cognitive
gain in number sense, conceptual development, and visualization can empower
and motivate students to engage in true mathematical problems solving at
a level previously denied to all but the most talented. The calculator
is an essential tool for all students in mathematics.
Approach and Methodology
The subjects for this study were from the students enrolled in three freshman
pre-calculus algebra classes at Macon College, a two-year institution, during
the spring quarter of 1997. The only prerequisite for the course was high
school Algebra II or college Developmental Studies Algebra.
The fifty-six students (82% of the total students in the class), ranged
in age from 18 to 68, with a mean age of 26 (25 w/o the 68-year-old).
91% of the students had gone through Algebra II in high school, with a mean
math grade of 2.5. 77% reported that they had taken a developmental studies
class within the last year with a mean grade of 2.9 (38% made an A). 48%
reported having used a calculator in high school and 54% used a calculator
in their developmental studies class. They reported studying math an average
of 6 hours a week. This studying was done alone by 62% and a combination
of alone and with others by 38%. 84% thought that mathematics was important
to their career plans. The following are the results from the question
"Has your attitude toward using the graphing calculator changed since
you started using it in this class?" No: 4% still did not like it,
19% liked using it previously, and 7% said no without any explanation.
Yes: 66% liked it better, overall, because they knew more about how to use
it and what it can do. One person (2%) said she was more frustrated with
the calculator than when the class started. One other person (2%) said
yes without an explanation.
The apparatus consisted of three parts. Part 1 was a series of personal
information questions. Part 2 was an attitude survey (not summarized or
analyzed in this paper). Part 3 consisted of six problems complete with
instructions.
Part 3 was distributed at the beginning of class. Orally, the students
were reminded to follow the general directions at the top of the page for
all problems. They were also told that this would in no way adversely affect
their grade. It should be noted that the drop date had passed when this
was administered, so all students taking part will finish the course. Each
concept within the questions had also been mentioned directly or indirectly
at some point in the quarter. Each class had 50 minutes to work the six
problems. In the interest of time, the students answered Parts 1 and 2
outside of class.
Outcomes
According to Butler & Wren (1965), there are four distinct types of
problem-solving difficulties: comprehension, structure, operation, and judgment.
Comprehension difficulties often occur when the student has a poor vocabulary
or reading ability. Inability to pick out hints and facts also reduces
comprehension. Structure difficulties arise when the student does not think
logically and critically enough to proceed to the solution. Operational
difficulties enter after the proper structure of the problem is present,
and the student cannot "effectively use the fundamental operations
necessary to arrive at a solution" (p. 380). Judgment difficulties
cause the student's inability to determine if the solution is reasonable
and correct. In reality, a student often experiences a combination of difficulties
when solving problems.
Each of the questions will be evaluated in relation to these difficulties.
The students were also asked if they used the calculator on each problem.
The use of the calculator will also be addressed.
Question 1:
You want to fence a rectangular plot bordering a building.
You only need three sides fenced because the building forms the fourth
side. If one side is 5 meters longer than an adjacent side, and you have
70 meters of fencing: Find the dimensions of the plot. Does this question
have anything to do with the maximum area of the plot? Why?
Comprehension was a problem for 21 of the 56. Eleven people did not attempt
to work the problem. One person even stated, "I can't do word problems."
Eight people let the 70 meters represent "area," and 2 people
used all 4 sides. Structurally, only two people realized that they could
orient the plot in two different ways, and one of those students did arrive
at both sets of dimensions correctly. Forty-six people did sketch a rectangle
and attempt to label it. Thirty-two students managed to set up an equation,
and 27 of those solved correctly for the variable. Twenty people gave a
correct set of dimensions. Understanding was also lacking in relation to
the maximum area inquiry. Nineteen people did not answer the question.
Twenty-one said yes because dimensions were involved. Sixteen said no
because the "question involved perimeter" or "it didn't ask
for area." In explaining why, the one person who found both sets of
dimensions, proceeded to find the area of each and identified the one with
the largest area. She further found the maximum area when 70 m of fencing
was used without the restriction that one side was 5 m longer than the other.
The judgment phase was attempted by ten people who checked their answers.
Nineteen people said they did not use the calculator mainly because it
involved easy arithmetic. Seventeen students did use the calculator to
do the arithmetic or to check the answer they obtained by hand.
Question 2:
A rope four meters long is cut into five pieces of equal
length. Is each piece longer or shorter than one meter? Why?
Six people did not attempt to answer the question. One person said "longer"
and one person said they were the "same length." Nine people
drew a rope and divided it into five pieces. The other 48 answered "shorter,"
showing class comprehension of only 86%. Those people also followed through
showing all phases through judgment with their explanation. Nine people
used their calculator citing "division" as the reason. Forty-two
people said they did not use the calculator for reasons such as, answer
was just common sense, division was basic and could be done easily by hand
or mentally.
Question 3:
A triangle has a perimeter of 42 inches. The medium length
side is twice as long as the shortest side and half as long as the longest
side. How long is each side?
Eleven people skipped the question leaving the remaining 45 students with
some level of comprehension. One person tried to use area instead of perimeter.
41 students sketched a triangle and 31 went on to the structure and operational
stages and set up an equation to obtain the numbers 6, 12 and 24. These
met the length relationship with a sum of 42. Judgement was incomplete
for everyone, as no one realized that a triangle would not be formed by
that arrangement of lengths. Eleven people said they used the calculator
to do the division or check the answer. 27 said they did not use the calculator
because it could be done mentally. Seven people noted you could not use
the calculator because this question required a drawing.
Question 4:
"An army bus holds 36 soldiers. If 1,128 soldiers are
being bused to their training site, how many buses are needed?" (Taken
from the National Assessment of Educational Progress (1983))
One person did not attempt the question. The remaining 55 people showed
comprehension and structural reasoning by dividing. Judgment proved difficult
for 21 individuals; seven answered 31_ buses and fourteen rounded down to
31 buses. Forty people used the calculator to do the division, while fifteen
did the division by hand. All obtained 31_, then drew their conclusion.
Question 5:
Compute
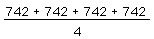
This problem is similar to the problem Schoenfeld quotes for Wertheimer
who believes the elementary age student should be able to look at the problem
and write as
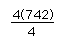
to illustrate true mastery of the operation (Schoenfeld, 1988).
All 56 students showed basic comprehension. Four people made computational
errors. Three of those errors were due to not entering parentheses in the
calculator. Those students then did not use judgment to realize that 2411.5
could not be the correct answer. Of the 52 students who arrived at the
742 for the solution, only 6 showed the step noted above. 39 people used
the calculator to find the answer saying it made the arithmetic go quicker.
It is of interest to note that two of those students went on to say that
they should have seen the obvious and not used the calculator. The other
17 did not use the calculator because the arithmetic was easy or obvious.
Question 6:
Given f(x) = 1 - 3x with Domain = {-3, -1, 0, 1, 3}. Which
number in the domain is associated with the highest point of the graph?
What is the range of the given function? Graph the given function.
Thirty-one students demonstrated comprehension through judgment here by
stating -3 was the answer because it was associated with the function value
of 10. Four people did not answer the question. Thirteen people answered
3 because it was biggest. The remaining eight students gave answers that
related to the graph such as intercepts. When asked for the associated
range, only twelve people showed comprehension by listing the set of values
{10, 4, 1, -2, -8}. Six students did not answer the question, and the remaining
40 gave various responses that showed little or no comprehension. Comprehension
was getting worse by the third part of the question. When asked to graph,
five people left it blank, and 48 drew a solid line. That 48 included 9
of the 12 who answered range with the set of separate points. Forty people
used the calculator to graph and thus explains the solid line. This is
consistent with Rich (1990) who found that students do not instinctively
use and understand graphs just because they have a graphing calculator.
Conclusions
There were breakdowns in each of the problem-solving phases by various
students. This is consistent with Butler, who states that students are
at different ability levels (Butler & Wren, 1965). This is still holding
true for the college freshman.
The traditional "army bus" problem seems to indicate that some
contextual realization does come with maturity. The 1983 NAEP showed 47%
of the 13-year-olds with as erroneous conclusion (Carpenter, et al., 1983).
The students in this study only showed 39% erroneous conclusions.
Physical maturity did not help in the problem Wertheimer said should be
evident to elementary age children. Only 11% of the college students exhibited
this trait.
In many cases, the student was satisfied just to get a number answer.
Lack of motivation may be a cause of students not moving on to the judgment
phase.
Use of the calculator seems consistent with prior use. 48% of the students
used a calculator in high school and 54% used a calculator in their developmental
studies class. The calculator was used in this survey in a variety of ways
for an average of 54% of solutions.
Lovell (1971) suggested that students develop their concept of function
in stages. In early stages, they can carry out an arithmetic relationship
in a table or on a line graph. In this stage they have difficulty translating
between graphical representations and ordered pairs. They progress to a
point where, in the final stage, the student has mastered the function concept
and can find domain and range. This may be the case in question six.
Some questions remain. Among them: (1) How are students motivated to want
to think through all the steps of problem solving difficulties? (2) Can
the graphing calculator to be used in this motivating process, and if so,
how?
References
Bitter, G. G., & Hatfield, M. M. (1991). Here's a math-teaching strategy
that's calculated to work. Executive Educator, 13,
19 - 21.
Butler, C. H., & Wren, F. L. (1965). The Teaching of Secondary
Mathematics (4th ed.). New York: McGraw Hill.
Carl, I. (1989). Essential Mathematics for the Twenty-first Century: The
Position of the National Council of Supervisors of Mathematics. Mathematics
Teacher, 82, 470 - 74.
Carpenter, T. P., Lindquist, M. M., Matthews, W., & Silver, E. A. (1983).
Results of the Third NAEP Mathematics Assessment: Secondary School. Mathematics
Teacher, 76, 652 - 659.
Carter, H. H. (1995). A visual approach to understanding the function
concept using graphing calculators (Doctoral dissertation, Georgia
State University, 1995). UMI # AAI9602812
Lovell, K. (1971). Some aspects of the growth of the concept function.
Piagetian Cognitive Development Research and Mathematics Education
(pp. 12 - 33). Washington, DC: NCTM.
Krulik, S. (Ed.). (1980). Problem Solving in School Mathematics.
(Yearbook of the National Council of Teachers of Mathematics). Reston,
VA: NCTM.
National Research Council. (1989). Everybody counts: A report to
the nation on the future of mathematics education. Washington,
DC: National Academy Press.
National Research Council. (1990). A challenge of numbers.
Washington, DC: National Academy Press.
National Research Council (1991). Moving Beyond Myths: Revitalizing
Undergraduate Mathematics. Washington, DC: National Academy Press.
National Council of Teachers of Mathematics. (1989). Curriculum
and Evaluation Standards for School Mathematics. Reston, VA: NCTM.
National Council of Teachers of Mathematics. (1996). Position Statement.
School Science and Mathematics, 96, 45.
Rich, B. S. (1990). The effect of the use of graphing calculators
on the learning of function concepts in precalculus mathematics
(Doctoral dissertation, University of Iowa). UMI # AAI9112475
Schoenfeld, A. (1988). When Good Teaching Leads to Bad Results: The Disasters
of "Well-Taught" Mathematics Courses. Educational Psychologist,
23(2), 145- 166.
Szetela, W. & Super, D. (1987). Calculators and Instruction in Problem
Solving in Grade 7. Journal for Research in Mathematics Education,
18, 215-229.

