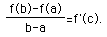
If y=f(x) is a continuous function on the closed interval [a,b] and differentiable on the open interval (a,b), then there is at least one number c between a and b at which

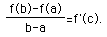
In figure 1 below, we can see that there is one place where there is a tangent line with a slope equal to that of the secant line. You may need to scroll right to see.

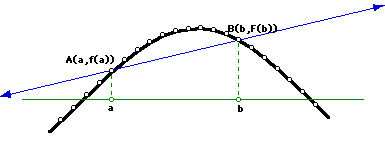
FIGURE 1

Our strategy for the proof is going to be to try and manipulate our interval by producing from it another function to which we can apply Rolle's Theorem. We can't apply it directly now because f(a) and f(b) in the mean value theorem need not equal each other nor zero.

What we need to look at is the function which measures the vertical distance between the secant line and the function f(x). The secant line is the function,

,

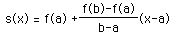using the point-slope line formula. The vertical distance between the function s and the function f is:

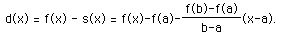
See figure 2 below which is a picture of the difference function.

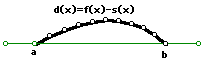
FIGURE 2

Notice how the endpoints have come down to the x axis.

The nice thing about d(x) is that Rolle's Theorem does apply to it, since f(a) = f(b) = 0. Therefore, d'(x) = 0 somewhere on (a,b) for some x=c. What does this say about f'(x)? If we differentiate d(x), we will find out.

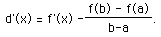
Now let x=c,

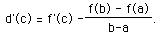
Remember at c, d'(c) = 0, so:

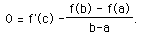
And with a little help from our resident algebraist we have,

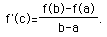
Q.E.D.

To return to the mean value theorem document, click more MVT. To return to the homepage, click loondog.