Prove that if every polynomial of degree 3 has at most 3 real roots, then every polynomial of degree 4 has at most five real roots.

Solution:

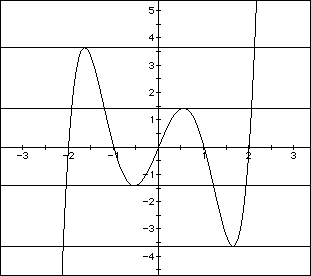
Rolle's theorem tells us that on an interval [a,b] which satisfies its conditions (review if necessary) when f(a) = f(b) = 0, there is at least one number c on the interval where f'(c)=0. Let f be our function of 4th degree. Assume that a polynomial of 4th degree has 5 real roots. Then between each pair of those roots there is at least one place where f' =0. Since f' is of degree 3, it has at most 3 real roots (a given). However, If f has 5 real roots and we pair them up adjacently, we find there must be at least 4 places where f' =0. See figure 1.

FIGURE 1

This contradicts our given. Therefore, our polynomial of 4th degree cannot have 5 (or more) real roots. It must have 4 or less.

Q.E.D.

Now, see if you can extend this argument (also using mathematical induction) to prove that an nth degree polynomial has at most n real roots.

CLICK MVT TO RETURN TO THE MEAN VALUE THEOREM DOCUMENT. CLICK loondog TO RETURN TO THE HOMEPAGE.