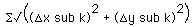
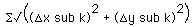
as k runs from 1 to n subintervals approximates the curve length, as we have seen. Our formula needs to get the rule of the function involved. This will produce simplification. Remember that the mean value theorem says that between on any such subinterval, there is a value of x, say c sub k, where the slope of the curve is equal to the slope of the secant line of the subinterval. Click "MVT" and use the "rot" point followed by dragging the tan line to find tangents to the pieces of the curve associated with the subintervals.
At the point c sub k , we have
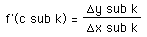 .
.
Solving, we have
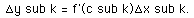
Using substitution, we now can write our sum as
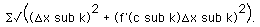
Factoring out a
 ,
,
and evaluating the square root of the same, we obtain
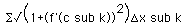 ,
,
as k runs from 1 to n subintervals. Voila! We have a Riemann sum. Now, let the widest subinterval of the partition (the norm) go to zero (as a limit), and we get a definite integral,
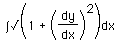 ,
,
evaluated from the left endpoint of the partition (a) to the right one (b). This integral gives us the length of the curve from a to b (in our picture, from -1 to 2). A similar formula can be developed for an integration along the y axis.
See if you can use the formula to show the length of the curve
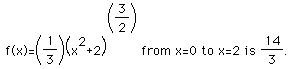
To return to the homepage, click " loondog.