N. J. Neer
Product and Packaging Design Dept.
Mob Eel Oil Co.

Dear Mr. Neer:

The vice president has decided that we are going to make changes to improve the bottom line of our company. One of these changes is to manufacture our own product containers.

What we need from your department is an analysis of the lowest cost container you can provide us to hold predetermined volumes of oil. These containers need to be right circular cylinders. Materials for construction will be expensive and must be held to a minimum. We trust you can design the packaging required at a reasonable price, or we may find ourselves improving our bottom line by worsening yours.

Sincerely,

Y.O. Boss
Junior Vice President
Mob Eel Oil

Well, you certainly have your work cut out for you, especially if you flunked Calculus at Ga. Tech, right? Obviously you need to hold the construction materials to a minimum. If only you can write an equation to represent the construction materials, you can try and minimize the value.

We know the top and bottom of a right circular cylinder are congruent circles. The area of a circle is

.

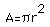The lateral surface area can be obtained by stacking up circumferences of the circular base. How many? That would be equal to the height, h. So, the lateral surface area is

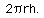
The entire surface area of our right circular cylinder is then

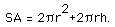
According to the memo, you are going to be provided with predetermined quantities (container capacities), say any individual quantity "Q". Q is a constant for any individual cylinder. How will this help us with the surface area equation? It eliminates a variable, right? Since the volume of such a cylinder is given by

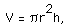
that is stacking up "h" circular base areas, then we have

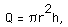
or

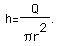
Substituting in our surface area formula, we have

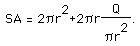
Simplifying we obtain

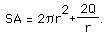
Let's check out a graph of this function. See if you can locate the radius which gives the minimum amount of surface area for the cylinder with capacity Q. Click investigate to do so now.

Well, did you find a suitable radius? Did you think about changing the value of Q (on the y axis)? Go back and try it now and see how doing so affects the function and therefore its graph. Click investigate.

Can calculus find these minimum values for you? Using what we have learned previously, take the derivative of SA. We have

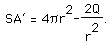
We do not expect an extremely tall skinny cylinder nor an extremely short fat one. An analysis of endpoints will show the surface area increasing near there. The equation is undefined when r = 0, however a cylinder of radius zero cannot be suitable for manufacture anyway. This leaves one possibility, set SA` equal to zero. Doing so we obtain

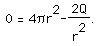
Calling on our resident algebraist, we have

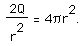
Solving for r we have

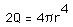
and

.

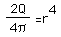Finally,

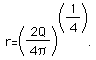
This value minimizes r for any constant cylinder capacity Q.

Click investigate again. Try your equation for r by plugging in the value of Q from the y axis. Does the resulting value of r agree with the graph on the screen?

In your own words, explain how the first derivtive produced the minimum for you.

Return to the "optimization" document.

Return to the homepage "loondog".