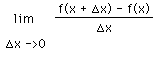
The idea of a limiting quantity intrigued mathematicians for centuries. Zeno, in his famous tortoise and hare paradox, certainly introduced the need for it in ancient Greece. Archimedes probably came closest (amazingly close for someone whose number system was not so neat as ours) to getting at the mathematics behind the notion of limit in olden days. Newton, in the use of his calculus, used the result of taking limits, but the mathematics needed to underpin the process was provided much later by Cauchy.

In the study of calculus, one must undertake to understand the concept of limit. After all, it is the engine which drives the derivative and the antiderivative. Just consider the definition of the derivative: given a function f, its derivative is a function f` which has a value at x of f'(x) =

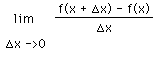
(provided the limit exists). (For more on this click Derivatives Are Cool.)

In order to have a derivative, you must evaluate this limit. In order to evaluate the limit, it must exist, and of course you must believe it exists.

So, what is a limit anyway? Keep in mind that we are not trying to prove a theorem when we discuss what a limit is. We have a new definition, the definition of limit. Informally, we can say that the limit of some function f(x), as x approaches some value c, is L if the values of f(x) approach L as x approaches c. Lets look at a simple case. Click "example" to do so.

Well, we have seen that in order for a limit to exist at a point, the left and right hand limits must exist and be equal. Also, the value of the limit at some x value sometimes equals the function value there; however, the limit may exist without the function value even existing at all. For an example click "example 2" now.

We have talked in example 2 about how having a limit means getting arbitrarily close. Let us put some formal mathematical legs under this notion. We will now take a look at what is called the delta-epsilon definition of limit. Click delta-epsilon to do so.

How did we guarantee that there is a delta for any radius e>0 about L for the function f(x) = 2x +1? It was done by choosing delta less than or equal to epsilon divided by 2. If need be, go back to delta-epsilon and click show to see the analysis.

Now try your hand at finding a suitable delta to prove that the limit as x approaches 2 of (3x - 4) is equal to 2.

Finding deltas is not always such a clean process. One must often employ more algebra, especially algebra of inequalities.

Let us look at a different function, a parabolic one. Click parabola now.

What exactly were you doing when you followed the instructions in the sketch? How can we truly show a delta exists for every epsilon? Let us solve the epsilon inequality.

.

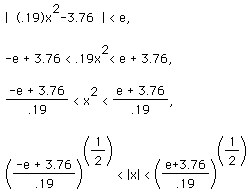So, in order to guarantee | f(x)-L | is less than any radius e about L, x must be in the range shown in the last equation above. These interval endpoints are the points a and b in the sketch (the x coordinates that go with L + e and L - e). When we pull x within the radius delta about xo, we want this last inequality to hold. We can guarantee this by making delta less than or equal to the smaller of

.

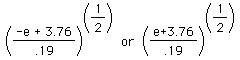This is what you were doing in the sketch. Now we can also find deltas algebraically for each epsilon we are faced with. This is way cool.

Now try your hand at following this reasoning to prove that

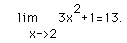
The actual evaluation of a limit at a particular value of x can involve direct substitution, algebraic manipulation followed by substitution, or other techniques and analysis.

For example, consider

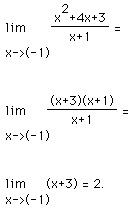
Notice the algebraic manipulation which removes the discontinuity at x = -1. The last function rule is perfectly good for the evaluation of our limit since we are not concerned with the value of the function at x=-1 (and therefore we stipulate x does not equal -1). We are concerned only with its limit. This allows us to evaluate the limit.

For another example, consider how you would evaluate the limit as x approaches zero of 1/x. Analyze what is happening, and one can tell that as the denominator of the fraction approaches zero, the overall fraction blows up (in fact, to infinity).

Limits are the foundation of the calculus. As previously stated, we cannot obtain a derivative without evaluating a limit.

Now try your hand at evaluating some limits.

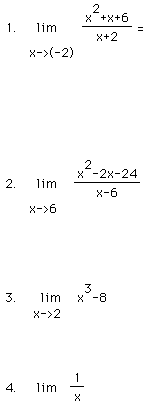
To return to the homepage, click " loondog".