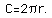
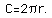
Taking the derivative of this equation gets the rates of change of the radius and the circumference involved. Doing so, we obtain
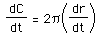 .
.
Solving for the change in the rate of change of the radius, we have
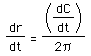 .
.
So, plugging in the givens we produce
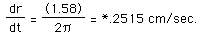
Now, click cir.squ and click "show". Then find the formula that is giving the answer in the sketch. Check your answer by setting dC/dt equal to 1.58. Explain the formula in the sketch.
To return to the related rates page, click " back".