It is not surprising that the trig functions have derivatives. If you know their curves very well, you can picture tangent lines at many points. Let's take a look at sinx and cosx and refresh our memory.

Let's get cosx down with sinx and look again!

Now, here is your beach bum question of the day. Have you ever seen a "tan" gent surfing a sine wave?

Now take a look at surfing tangents side by side on a sine and cosine wave. Watch the values of the tan slopes and carefully compare them to the values of the functions. Your mission, should you choose to accept it, is to produce some proposition about the first derivative of sinx and cosx. This paragraph will selfdestruct when you click "mission".

Wasn't an impossible mission, was it? Did you "cruise" right to a conjecture? The slopes of the tan lines are of course the derivatives at the chosen x value. Did you see that the derivative of sinx is cosx, and the derivative of cosx is -sinx? Go "back" and look again.

For a little more inductive evidence, let's take a spreadsheet look at the derivative of sinx. Click "new look".

Can you prove that the derivative of sin(x) is cos(x)? Start with a statement from the definition of the derivative, and proceed from there. Afterwards, scroll on down for a proof.

J

E

O

P

A

R

D

Y

T

H

E

M

E

Q.E.D. (Latin for Quite Educational Dude?)

Try now to prove that the derivative of cosx is -sinx using the definition.

How might you find the derivative of tangent? Work on this for a few moments. Then scroll down to see (Hint: Write tanx = (sinx)/(cosx).)

J

E

O

P

A

R

D

Y

M

U

S

I

C

See if you can find the derivatives of the following..........................

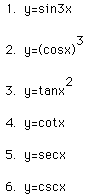
To return to the homepage, click " loondog".