---

---

---

Another Geometric Approach

---

 

Consider a circle with chords AB and CD. Let the CD pass through the midpoint M of AB.

Let AM = MB = z and let CM = x, MD = y. The lengths are all positive values.

By an elementary theorem of geometry the products of the parts of the chords are equal. That is,

Construct the perpendiculars from center of the circle to the midpoints of the respective chords. The distance to AB is d and the distance to CD is c.

If M is not the center of the circle, we know c < d and so x + y > 2z . . . therefore

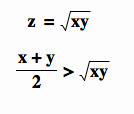
. . . but, if M is the center of the circle, then c = d = 0, or x = y, in which case

Adapted from Sidney H. Kung, The College Mathematics Journal, Vol. 26, No. 1, Jan. 1995.