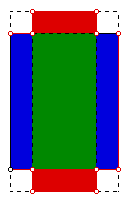
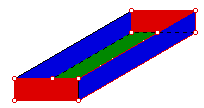
Problem:
*Use the Arithmetic Mean-- Geometric Mean Inequality to find the maximum
volume of a box made from a 25 by 25 square sheet of cardboard by removing
a small square from each corner and folding up the sides to form a lidless
box.


*Use the AM--GM Inequality to determine what shape boxes could be created
by this method from the 25 by 25 square sheet to hold a volume of 100 cu.
units? 200 cu. units? 400 cu. units?
*Generalize. Use the AM--GM Inequality to discuss the maximum volume of
a box formed from an n X n square sheet of cardboard.
*Why will the AM--GM Inequality not be a useful tool when the sheet of cardboard
is 20 by 25?
To find the maximum volume, x, (25-2x), and (25-2x) must sum to a constant
and they should be equal to one another. To meet these conditions, we need
to multiply our volume equation by 4/4.
Our inequality is
To find the maximum volume,
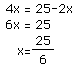
Now, the maximum value occurs when x =25/6.
The maximum volume is 1156.41 cu. units.
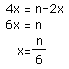
For any n X n square, the maximum volume occurs when x=n/6.