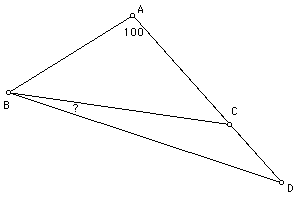
PROBLEM: Hundred Degree Isosceles Triangle
Given an isosceles triangle ABC with AB = AC and the measure of angle BAC
= 100 degrees. Extend AC to point D such that AD = BC. Now draw segment
BD. What is the size of angle CBD?
Discussion/Solution?:
Construct an equilateral triangle ADE with a side AD and side BE in the
interior of angle BAD.
Draw BE.
Each angle of triangle ADE has measure 60, so measure of angle BAE = 40.
We were given AD = BC. We now have AD = DE = EA (by definition of an equilateral
triangle). Thus,
BC = EA.
Note also that measure of angle BAE = 40 = measure of angle ACB and that
BA = AC (if base angles of a triangle are equal, then the sides opposite
those angles are equal). Therefore,
triangle BAC is congruent to triangle EBA.
By corresponding parts of congruent triangles, BE = BA. Also, BD = BD
by the reflexive property of equality. So
triangle BAD is congruent to triangle BED
by SSS. This leads to
measure of angle ADB = measure of angle EDB
by corresponding parts. Since measure of angle ADE = 60 , then measure
of angle ADB = 30. Thus
measure of angle CBD = 10
(the sum of the angles in a triangle equals 180).
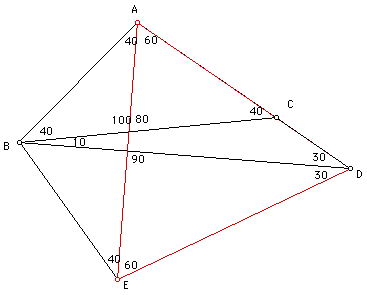
Note the type of angle formed by the intersection of AE and BD.
By labeling the angles in the diagram and using the fact that the sum of
the angles in a triangle must equal 180, we find that the angles formed
by the intersection of AE and BD are right angles.
Return to Susie Lanier's Class Page.


