PROBLEM: Circular Window
Use compass and ruler to construct the following design of a circular window.
How can it be constructed?
What fraction of the area of the circle is in the "triangular"
region in the center bounded by the three arcs?

Discussion/Solution?:
Construct the circular window:
- Draw a circle of any radius.
- Draw any diameter of the circle.
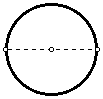
- Construct two more diameters of the circle with the angle between
each diameter being 60 degrees.
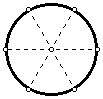
- Construct a circle through one of the points on the original circle
and tangent to the other two diameters.

- Construct the desired arc through the three points (the point on the
original circle and the two tangent points on the diameters.
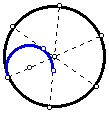
- Rotate the arc 120 degrees (twice)
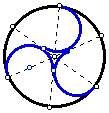
- We now have the desired figure

Now let's turn our attention to the "triangular" region in
the center.

We want to determine the fraction of the area of the original circle
that that is covered by the "triangular" region bounded by the
three arcs.
Let r = the radius of the original circle.
Let 2x = the side of the triangle joining the centers of the incsribed
circle
So x = the radius of an inscribed circle
Relate x to r ----
Return to Susie Lanier's Class Page.








