W. Courtney Trabue
EMT-725 Problem Solving
Dr. Jim Wilson (Spring 1997)
Problem Statement:

Given an isosceles triangle ABC with AB = AC and the measure of angle BAC = 100 degrees. Extend AB to point D such that AD = BC. Now deaw segment CD.
Construction: Let A be the center of a circle with radius BC.

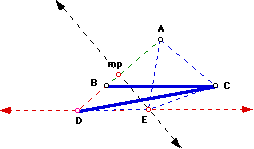
What is the size of angle BCD?


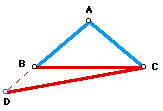
Draw Angle ADE congruent to Angle ABC by extending a Ray from D parallel to BC. Construct a perpendicular bisector of segment AD, which will intersect the Ray extending from D at point E.

Connect point E to A with a segment.

By construction we now have:

DE = AE = AB = AC

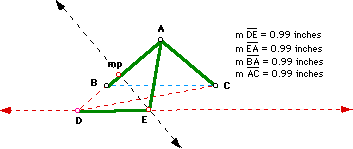
Now connect point E to C.

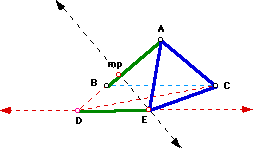
But Triangle AEC is equalateral.

So DE = AE = AC = EC and

Triangle DEC is isosceles with Angle DEC = 100 + 60 = 160.

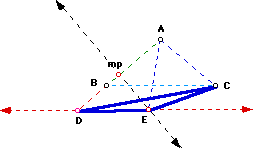
Triangle DEC is isosceles with Angle DEC = 100 + 60 = 160.

Therefore, Angle EDC = 1/2 (20) = 10

so Angle BCD = 10 because it is an alternate interior angle.

Return to Court's Home Page.