W. Courtney Trabue GMC-AUGUSTA Community College Department of Mathematics 115 Davis Road Martinez,GA 30907 |
|
EMT-725 Problem
Solving Dr. Jim Wilson (Spring 1997) |
|
Problem Statement: How do you minimize the surface area of a right circular cylinder for a given volume? |
|
Solution: The Algebra We know from high school algebra that the volume and surface area of a right circular cylinder can be calculated from the following formulas: (1) (2) Now, by rearranging (1) into:
and substituting
which reduces to:
and by factoring out the 2 we get: (3) It is easy to see that as r increases, the ratio V/r
decreases and |
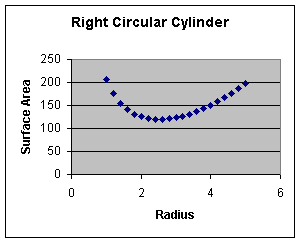
Solution: The Graph Since the two parts of the equation behave in opposite fashion, we could assume the graph has a turning point. If we fix V=100, and graph the Surface Area equation using Microsoft Excel 2000
we can see this point. It is the Minimum for Surface Area. Using the built in “MIN Function” of Excel, we find that S is approximately minimized at 119.3974 when r = 2.6. This procedure could be refined by reducing the incremental change in r to render a more accurate approximation Extended this Investigation: Try using different fixed values for V (200, 300, 400, etc.) and plot the XY-coordinates of the minimums. What kind of graph is generated? Can you explain its significance in the context of the original problem? |
for 
into (2), we get
increases. If r increases without bound, V/r approaches
“zero” and 
