Minimum of f(x)

W. Courtney Trabue
EMT-725 Problem Solving
Dr. Jim Wilson (Spring 1997)

Problem Statement:

Use the Arithmetic Mean -- Geometric Mean Inequality to show that
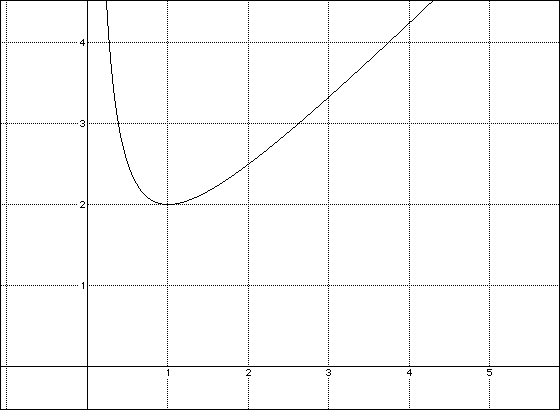
Min f(x) = 1/x + x is 2.

Solution:

The inequality is true for non-negative varaibles.

To find the minimum value of f(x) for positive values of x, the AM-GM Inequality is:

Arithmetic Mean Geometric Mean

(1/x + x)/2 [> or =] [(1/x ) x]^(1/2)

Multiplying both sides by 2 generates

1/x + x [> or =] 2(1) = 2

f(x) [> or =] 2.

This neans that for positive values of x, the minimum value of f(x) is 2.

This occurs when 1/x = x. (i.e., when x = 1.)

Using Algebra Expresser to graph this relationship we get a minimum point at (1,2).

Return to Court's Home Page.