W. Courtney Trabue
EMT-725 Problem Solving
Dr. Jim Wilson (Spring 1997)
Problem: Construct the largest square possible in a given right triangle.

Two approaches are possible. The square could touch two sides of the given triangle, or just one side of the given triangle.

Approach # 1: Two sides of the Square lie on sides of the triangle.

Construction: Start with a right triangle ABC and bisect the right angle with a ray cutting the hypotenuse AB at point P. Construct lines perpendicular to the two legs, CB and CA, through point P. Connecting the intersect points ( a on CB, and b on CA) with vertex C and point P gives a Square.

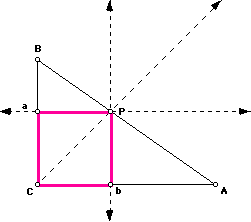
Approach # 2: Only one side of the square lies on a side of the triangle.

Construction: Take any right triangle ABC and pick a point P on the hypotenuse. Draw a line m perpendicular to the hypotenuse CB through P, which intersects the base AB at x1. Construct a circle with center P and radius length Px1. The circle will intersect the hypotenuse at x2. Use Px1 and Px2 as two sides of a square.

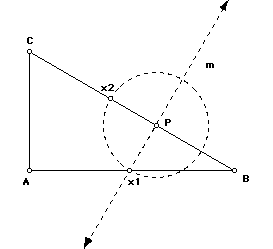
By constructing a line paralled to the hypotenuse through x1 and a line parallel to line m through x2 you get point of intersection which will form the 4th Vertex of a square.

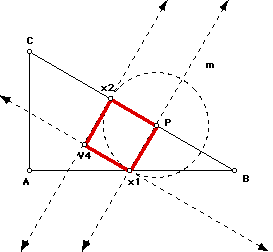
By extending a ray from B through x4 which intersects AC at V1 you get one of the vertices of the square. Construct a perpendicular through V1 to the hypotenuse of triangle ABC and the point of intersection will be the second vertex of your square. Use the distance from V1 to V2 as the radius of a circle with center V2. The circle will intersect the hypotenuse at V3 forming the third vertex of your square. Finally, construct a line parallel to V1V2 through V3. It intersects the base AB of the triangle at V4, the fourth vertex of the square.

Problem Solution: By constructing two identical triangles with GSP and inscribing a square in each one with different orientations we get area measurements for the squares that differ.

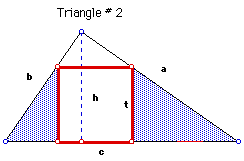
Now, we have two identical triangles with sides a, b, hypotenuse c, and altitude h. And, we have a square of side s inscribed in Triangle # 1 and a square of side t inscribed in Triangle # 2.

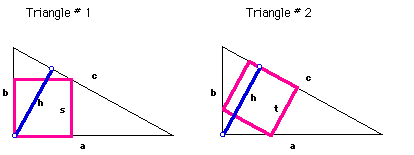
By reorienting Triangle # 2, and using the shaded areas to form a new triangle, then by similar tirangles we have




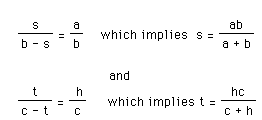
Since hc and ab are both twice the area of the original triangle, they are equal. So we need to compare the denominators of the relationships above to determine which one is smaller than the other.


Return to Court's Home Page.