W. Courtney Trabue
EMT-725 Problem Solving
Dr. Jim Wilson (Spring 1997)

Problerm Statement:
Part 1: Use the Arithmetic Mean - Geometric Mean Inequality to find the maximum volume of a box made from a 25 by 25 square sheet of cardboard by removing a small square from each corner and folding up the sides to a lidless box.

Let V equal the volume of the box. Then V = x ( 25 - 2x ) ( 25 - 2x ). This equation can be
rewritten as V = 1/4 ( 25 - 2x ) ( 25 - 2x ) ( 4x ) which must be < or = ( 1/4 ) ( 50/3 )^3, which is equal to 1157.407.

The following Algebra Expressor graph supports this finding.

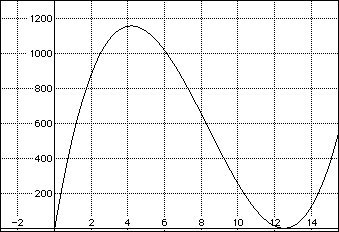
Using the Excel Spreadsheet with step size 0.5 we get the following view of the problem.

Part 2: Use the AM - GM Inequality to determine what shape boxes could be created by this method from the 25 x 25 square sheet to hold a volume of 100 cu. units; 200 cu. units; 400 cu. units.

Using the same approach as before where V = x ( 25 - 2x) ( 25 - 2x), the inequality generates
( 50 - 4x + x ) / 3 > or = [ x ( 25 - 2x) ( 25 - 2x) ] ^ (1 / 3 ). By substituting 100 in for [ x ( 25 - 2x) ( 25 - 2x) ] we get ( 50 - 3x ) > or = 100 ^ (1 / 3 ). This simplifies to x < or = 12.026

I have confidence in this answer because the sides of the box must be positive. ( i.e. 25 - 2x > 0 )
which implies that x < 12.5 Since x must also be positive (i.e. x > 0 ) if the box is to have any volume. This same argument would be true for boxes of volume 200 and 400.

So if V = 200 we get 200 = x ( 25 - 2x ) ^ 2 which implies x = 10.99 when y = 0

 

Part 3: Generalize. Use the AM - GM Inequality to discuss the maximum volume of a box formed from an n X n square sheet of cardboard.

V = x(n - 2x)^2 = [4x(n - 2x)^2]/4
(1/4)(2n/3)^3 > or = (1/4) [4x(n - 2x)^2]
(1/4)(2n/3)^3 > or = x(n-2x)^2

The maximum value is (1/4)(2n/3)^3.

This occurs when 4x = n - 2x, or when x = n/6.

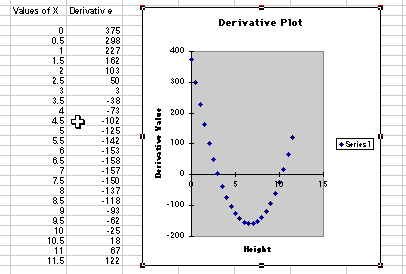
Using calculus and the concept of the derivative can accpmplish the same thing.

V = x(n - 2x)^2

V ' = 2(n - 2x)(-2)x + (n - 2x)^2

Setting V ' = 0 lets us calculate local max and min points.

0 = -4x (n - 2x) + (n - 2x)^2

0 = (n - 2x)[-4x + (n - 2x)]

0 = (n - 2x)(n - 6x)

0 = n - 2x = 0 or n - 6x

n/2 = x

n/6 = x

x= n/2 gives a volume of 0, so the maximum volume occurs when x = n/6.

Part 4: Why will the AM - GM Inequality not be a useful tool when the sheet of cardboard is 20 by 25?

V = x(20 - 2x)(25 - 2x)

V = (1/4) (4x)(20 - 2x)(25 - 2x)

V < or = (1/4) (45/3)^3 = 843.75

Now you should also be able to do this with

x = 20 - 2x = 25 - 2x.

There is no x value that will satisfy these equations.

20 - 2x = 25 - 2x

implies that 20 = 25 which is false.


Expanded Investigations

Modification to the Problem Statement:

Given a rectangular sheet of cardboard 15 in by 25 in. If a small square of the same size is cut from each corner and each side folded up along the cuts to form a lidless box, what is the maximum volume of the box?

We know from high school algebra the volume of a box is given by multiplying its lenght, width and height.

Volume = Length x Width x Hieght

 

For this problem, we cut a square size X ( for the height of the box ) from each corner, and fold up the sides.

This gives us the following: Height = X, Width = 15-2X, Length = 25 - 2X

 

 

 


Approach # 1

Algebra Xpresser

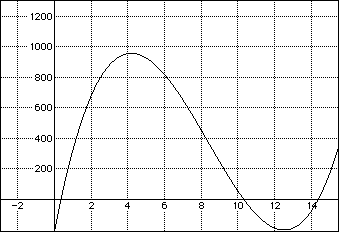
Using the equation y = x (25 - 2x) (15 - 2x) for the volume of the given lidless box, Algebra Xpresser generated the following graph.

ZOOMing in on the local maximum on the interval [0 , 7.5]

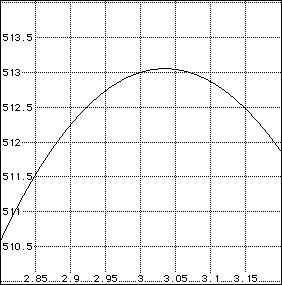
we can see that at x = a little more than 3, y = a little more than 513. Since the dimentions are in inches, the maximum volumn is a little more than 513 cubic inches.

Approach # 2

Algebra and the Excel Spread Sheet

Using the same equation the volume is V = X (25 - 2X) (15 - 2X).

By letting X vary in size from 0 to 7.5 (the max size of a cut out square is 15/2) and simultaneously calculating V in an Excel Spread Sheet we can get an idea of what's going on.

Graphing the results gives a visual solution to the problem. It appears to have a maximum
volume somewhere around 500 cubic inches.

By rescaling the spread sheet values for X in increments of .01, and investigating the interval

[ 2.9 , 3.14 ] we get the following results.


 

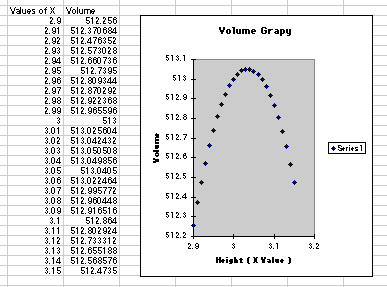
This approach lets us zero in somewhere in the neighborhood of X = 3.03 , give or take a little.


Approach # 3

Geometer Sketch Pad

When using GSP to solve this problem the dimensions must be scaled down.

The ratio of 15 : 25 = 3 : 5

Using GSP, open boxes of different sizes (volumns) can be developed by varying segment x.

The maximum volume of 520.12 cubic inches was obtained when x = 3.03 inches.

This agrees with the previous investigation using Algebra Xpressor.


Approach # 4

The Calculus Approach

We know from freshmen calculus that taking the derivative of a function and setting it to zero will give us local maxima and minima points.

For this problem the original function:

can be expanded to

Taking the derivative with respect to X, we get

Setting the derivative equal to zero locates the local max and min points.

Solving by ZOOMing in with step size h = .01

This gives us an x = 3.03 for the max voulme.

Go back to my Home Page