
Problem Proceedure: Construction
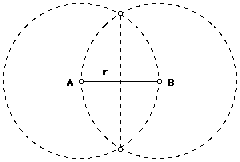
Construction: Begin with line segment AB and construct two circles with
centers at A and B and having radius r equal to the distance between AB.
Locate the points of intersection between the two circles and connect with
a segment. This segment will intersect segment AB at its midpoint.
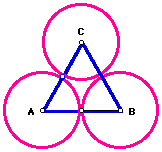
Now construct two tangent circles with centers at A and B, but with new
radius as the distance from A to the midpoint on AB.

Now construct a segment between point A and C. This segment will be bisected
by the circle with its center at A. Using the point C as the center of a
third circle with radius of 1/2 length segment AC we get the following diagram.

Removing the construction lines reveals three tangent circles of identical
size whose connected centers forms an equalateral triangle.
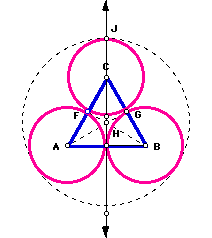
Now we connect the centers of circle A and B to the points of tangency
with circle C, forming two segments AG and BF, which intersect at point
H. By constructing a line through point H and C we can locate point J on
circel C. By constructing a segment between points H and J, and using its
length as the radius of a new circle we will call circle H, we can inscribe
the three tangent circles with a single circle.
To complete a diagram of the original problem we simply remove selected
portions of the above diagram and use the arc construction feature of GSP.

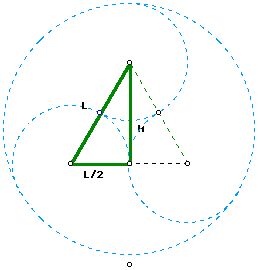
ANALYSIS: The area of the original equalateral triangle can be
calculated by the standard
formula of one half base times height. The base in this case is labeled
L, which is the distance between the centers of any two of the three inscribed
circles. The heigth of the triangle is labeled H and can be found using
the Pythagorean Theorem.
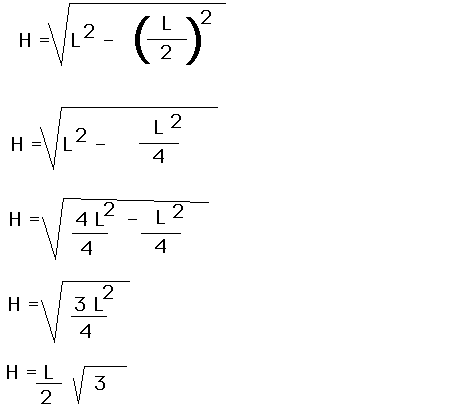
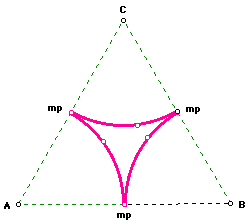
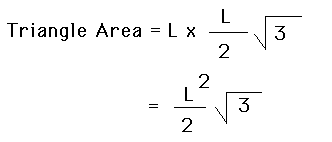
Each of the pie shaped wedges cut out of the area of the triangle represent
one-sixth of the area of one of the inscribed circles used in the original
conctruction.
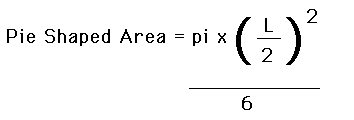
The area left in the center of the picture above can be calculated by
subtracting the three pie shaped wedges form the triangular area. With a
little algebra you get the following results.

Return to Courts Home Page